Варианты ЕГЭ профиль (с разбором)
Содержание
Вариант ЕГЭ профиль 1.19
Среди 1050 учеников школы 30% − ученики начальной школы. Среди учеников средней и старшей школы 20% изучают немецкий язык. Сколько учеников в школе не изучают немецкий язык, если в начальной школе он не изучается?
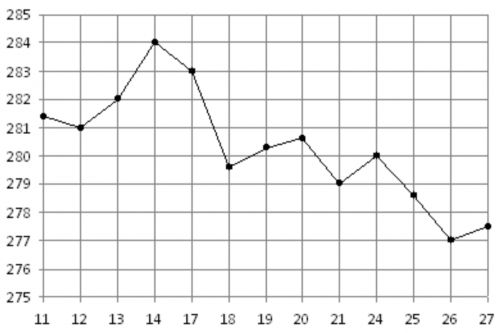
На рисунке жирными точками показана цена золота, установленная Центробанком РФ во все рабочие дни с 11 по 27 июля 2000 года. В выходные дни цена не менялась. По горизонтали указываются числа месяца, по вертикали – цена золота в долларах за унцию. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней за данный период цена золота не превышала 279 долларов за унцию.
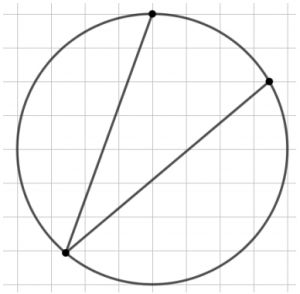
На рисунке изображен вписанный угол. Найдите тангенс смежного с ним угла. В ответ укажите квадрат этого числа, округлив результат до тысячных.
В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,7 погода завтра будет такой же, как и сегодня. 13 мая погода в Волшебной стране хорошая. Найдите вероятность того, что 15 мая в Волшебной стране будет отличная погода.
Решите уравнение \(\log_5(17-2x)=3\log_{25}4\)
Основания равнобедренной трапеции равны 52 и 39. Тангенс острого угла равен \(\dfrac7{13}\). Найдите высоту трапеции.
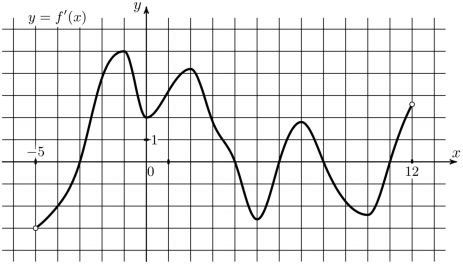
На рисунке изображён график \(y=f'\left(x\right)\) – производной функции \(f\left(x\right)\), определённой на интервале \(\left(-5; 12\right)\). Найдите количество точек максимума функции \(f\left(x\right)\), принадлежащих отрезку \(\left[-4;11\right]\).
Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны \(2\sqrt{3}\) и наклонены к плоскости основания под углом 30°.
Найдите значение выражения \(\dfrac{(\sqrt3 x)^{14}\cdot \sqrt[5]{x^5}}{(\sqrt[3]{x^5})^{9}}\) при \(x=\sqrt2\).
Скейтбордист прыгает на стоящую на рельсах платформу, со скоростью \(v= 3{,}6\, м/с\) под острым углом \(\alpha\) к рельсам. От толчка платформа начинает ехать со скоростью \(u=\dfrac{m}{m+M}\cdot v\cdot \cos \alpha\) (м/с), где \(m=70\, кг\) − масса скейтбордиста со скейтом, а \(M= 350 \,кг\) − масса платформы. Под каким максимальным углом \(\alpha\) (в градусах) нужно прыгать, чтобы разогнать платформу не менее чем до \(0{,}3 \,м/с\)?
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 154 км. На следующий день он отправился обратно со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Найдите наибольшее значение функции \(y=-2\mathrm{tg\,}x+4x-\pi+14\) на отрезке \(\left[-\dfrac{\pi}{3};\dfrac{\pi}{3}\right]\).
а) Решите уравнение \(2\sin\left(x+\dfrac{\pi}3\right)+\cos 2x=\sqrt3\cos x+1\)
б) Найдите все его корни, принадлежащие отрезку \(\left[-3\pi;-\dfrac{3\pi}2\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -3π | 18. -17π/6 | 19. -11π/4 | 20. -8π/3 |
| 21. -5π/2 | 22. -7π/3 | 23. -9π/4 | 24. -13π/6 |
| 25. -2π | 26. -11π/6 | 27. -7π/4 | 28. -5π/3 |
| 29. -3π/2 |
В правильной четырёхугольной призме ABCDA₁B₁C₁D₁ сторона основания равна 11, а боковое ребро АА₁= 7. Точка К принадлежит ребру В₁С₁ и делит его в отношении 8:3, считая от вершины В₁.
а) Постройте сечение этой призмы плоскостью, проходящей через точки В, D и К.
б) Найдите площадь этого сечения.
Решите неравенство \(\log_{7}(8x^2+7)-\log_7(x^2+x+1)\geqslant \log_7\left( \dfrac{x}{x+5}+7\right) \)
В трапеции\(ABCD\) с прямым углом \(A\) расположены две окружности. Одна из них касается меньшего основания \(BC\) и боковых сторон, а другая – большего основания \(AD\), боковых сторон и первой окружности. Прямая, проходящая через центры окружностей, пересекает большее основание в точке \(P\).
а) Докажите, что \(AP:PD=\sin D\);
б) Найдите площадь трапеции, если радиусы окружностей \(\dfrac13\) и \(\dfrac43\).
В июле планируется взять кредит на сумму 6 409 000 рублей. Условия его возврата таковы:
– каждый январь долг возрастает на 12,5% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен двумя равными платежами (то есть за два года)?
Найдите все значения параметра \(a\), при который уравнение \(8a+\sqrt{7+6x-x^2}=ax+4\) имеет единственное решение.
В школах №1 и №2 учащиеся писали тест. Из каждой школы тест писали по крайней мере 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешёл из школы №1 в школу №2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе №1 уменьшиться в 10 раз?
б) Средний балл в школе №1 уменьшился на 10%, средний балл в школе №2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе №2 равняться 7?
в) Средний балл в школе №1 уменьшился на 10%, средний балл в школе №2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе №2.
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.


