Задачи ЕГЭ профиль
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.
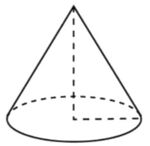
Диаметр основания конуса равен 40, а длина образующей – 25. Найдите высоту конуса.
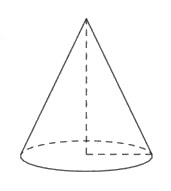
В правильной четырехугольной пирамиде SABCD точка O - центр основания, S - вершина, SA=10, BD=16. Найдите длину отрезка SO.
Найдите объем прямоугольного параллелепипеда, ребра которого равны 3, 5, 6.
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующая увеличится в 3 раза, а радиус основания останется прежним?
Во сколько раз уменьшится объём конуса, если его высота уменьшится в 9 раз, а радиус основания останется прежним?
Во сколько раз увеличится объем пирамиды, если её высоту увеличить в четыре раза?
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 9. Найдите объём цилиндра.
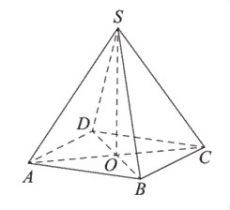
В правильной четырехугольной пирамиде SABCD с вершиной S точка O - центр основания, SO=35, SD=37. Найдите длину отрезка BD.
