Задачи ЕГЭ база
- 1. Простейшие текстовые задачи
- 2. Величины и значения
- 3. Графики, диаграммы, таблицы
- 4. Вычисления по формуле
- 5. Теория вероятностей
- 6. Выбор подходящих вариантов
- 7. Функции и производные
- 8. Выбор утверждений
- 9. Фигуры на квадратной решетке. Координатная плоскость
- 10. Прикладные задачи по геометрии
- 11. Стереометрия. Тела вращения
- 12. Планиметрия
- 13. Стереометрия. Многогранники
- 14. Вычисления с дробями
- 15. Проценты и пропорции
- 16. Значения выражений
- 17. Уравнения
- 18. Неравенства и числовая прямая
- 19. Свойства чисел
- 20. Текстовые задачи
- 21. Нестандартные задачи
7. Функции и производные (Задачи ЕГЭ база)
На графике изображена зависимость крутящего момента двигателя от числа оборотов в минуту. На горизонтальной оси отмечено число оборотов в минуту, на вертикальной оси – крутящий момент в Н⋅м.
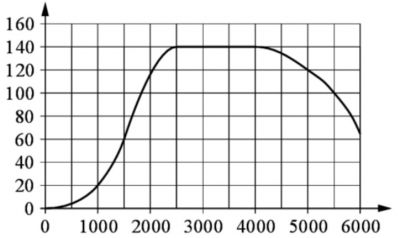
Пользуясь графиком, поставьте в соответствие каждому интервалу числа оборотов в минуту характеристику крутящего момента.
| ИНТЕРВАЛЫ | ХАРАКТЕРИСТИКИ |
| А) 0 - 1000 об./мин. | 1) Самый быстрый рост крутящего момента при увеличении числ оборотов |
| Б) 1500 - 2000 об./мин. | 2) При увеличении числа оборотов крутящий момент падает |
| В) 3000 - 4000 об./мин. | 3) При увеличении числа оборотов крутящий момент не меняется |
| Г) 4000 - 6000 об./мин. | 4) Крутящий момент не превышает 20 Н⋅м на всем интервале |
На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее с момента запуска двигателя, на оси ординат - температура двигателя в градусах Цельсия. Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику процесса разогрева двигателя на этом интервале.
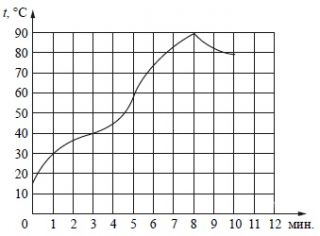
| Интервалы времени | Характеристики процесса |
| А) 0 - 2 мин. | 1) температура росла медленнее всего |
| Б) 2 - 4 мин. | 2) температура падала |
| В) 4 - 6 мин. | 3) температура росла быстрее всего |
| Г) 8 - 10 мин. | 4) температура не превышала 40° |
На рисунке точками показана среднесуточная температура воздуха в городе N в январе некоторого года. По горизонтали указываются числа месяца, по вертикали – температура в градусах Цельсия. Для наглядности точки соединены линией.
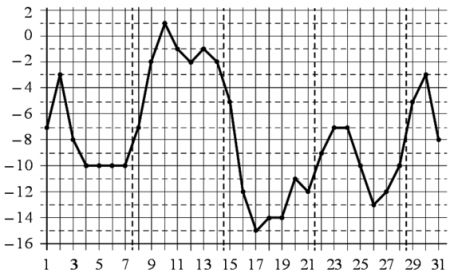
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику изменения температуры. Ответ запишите в порядке, соответствующем буквам АБВГ.
| ПЕРИОДЫ ВРЕМЕНИ | ХАРАКТЕРИСТИКИ |
| А) 1–7 января | 1. среднесуточная температура не поднималась выше -7° |
| Б) 8–14 января | 2. во второй половине недели среднесуточная температура не менялась |
| В) 15–21 января | 3. среднесуточная температура достигла месячного минимума |
| Г) 22–28 января | 4. среднесуточная температура достигла месячного максимума |
На графике показано изменение температуры в зависимости от времени в процессе разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее с момента запуска двигателя, на оси ординат - температура двигателя в градусах Цельсия.
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику процесса разогрева двигателя на этом интервале.
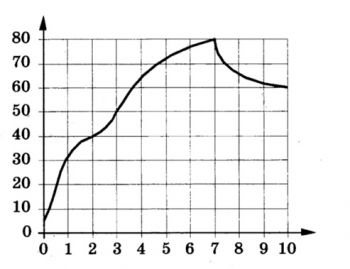
| ХАРАКТЕРИСТИКА ПРОЦЕССА | ИНТЕРВАЛ ВРЕМЕНИ |
|---|---|
| А) температура падала быстрее всего | 1) 0-1 мин |
| Б) температура падала медленнее всего | 2) 7-8 мин |
| В) температура росла быстрее всего | 3) 5-7 мин |
| Г) температура превышала 70°С | 4) 8-10 мин |
На графике изображена зависимость скорости движения рейсового автобуса от времени. На вертикальной оси отмечена скорость автобуса в км/ч, на горизонтальной - время в минутах, прошедшее с начала движения автобуса.
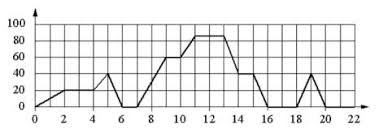
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику движения автобуса на этом интервале.
| ИНТЕРВАЛЫ ВРЕМЕНИ | ХАРАКТЕРИСТИКИ ДВИЖЕНИЯ |
| А) 4-8 мин. | 1) автобус не увеличивал скорость на всём интервале |
| Б) 8-12 мин. | 2) автобус ни разу не сбрасывал скорость |
| В) 12-16 мин. | 3) была остановка длительностью 2 минуты |
| Г) 16-20 мин. | 4) скорость не больше 40 км/ч на всём интервале. также была остановка длительностью ровно 1 минута |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам АБВГ.
Материальная точка движется прямолинейно по закону \(x(t)=t^2-13t+23\) (где \(x\) – расстояние от точки отсчета в метрах, \(t\) – время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?
На рисунке изображен график функции \( y = f (x)\) и отмечены точки А, В, С и D на оси \(x\). Пользуясь графиком, поставьте в соответствие каждой точке характеристику функции и ее производной.
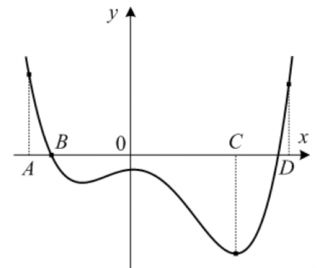
1. Производная равна 0, функция отрицательна;
2. Производная положительна, функция положительна;
3. Производная отрицательна, функция равна 0;
4. Производная отрицательна, функция положительна
На рисунке изображены график функции и касательные к нему в точках с абсциссами A, B, C, D. Поставьте в соответствие каждой точке значение производной функции в ней.
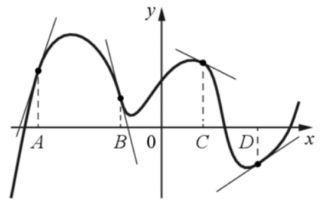
1. -0,5
2. 2/3
3. -4
4. 3
Установите соответствие между графиками функций и характеристиками этих функций на отрезке [-1;1].
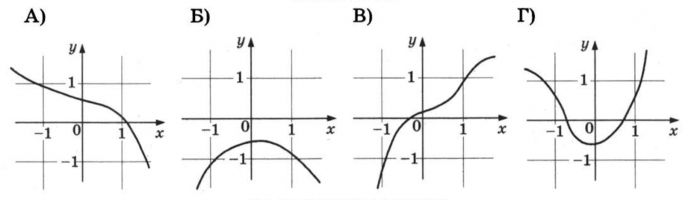
1) Возрастает на отрезке [-1;1].
2) Убывает на отрезке [-1;1].
3) Имеет точку минимума на отрезке [-1;1].
4) Имеет точку максимума на отрезке [-1;1].
Запишите в ответ цифры в порядке , соответствующем буквам АБВГ без пробелов и дополнительных символов.
На рисунке изображен график функции \(y = f(x)\). Установите соответствие между интервалами числовой оси \(OX\) и свойствами функции на этом интервале.
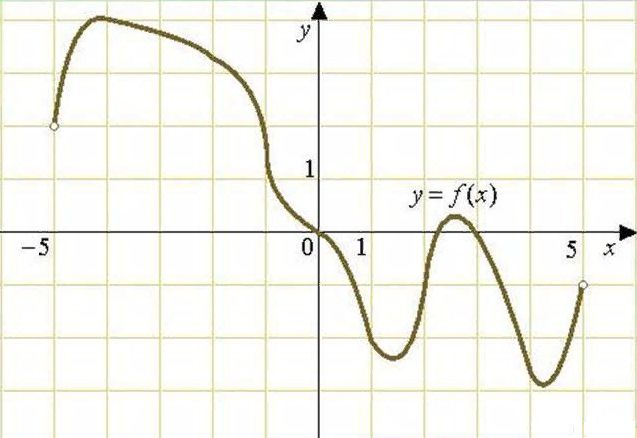
| А) \((-5;-1)\) | 1) Функция убывает на всем интервале |
| Б) \((-1;1)\) | 2) Функция имеет 2 точки экстремума на интервале |
| В) \((1;3)\) | 3) Функция отрицательна на всем интервале |
| Г) \((3;5)\) | 4) Функция положительна на всем интервале |