Задачи ЕГЭ база
Пирамида Хеопса имеет форму правильной четырёхугольной пирамиды, сторона основания которой равна 230 м, а высота – 147 м. Сторона основания точной музейной копии этой пирамиды равна 23 см. Найдите высоту музейной копии. Ответ дайте в сантиметрах.
Аквариум имеет форму прямоугольного параллелепипеда с размерами 80 см × 30 см × 40 cм. Сколько литров составляет объём аквариума? В одном литре 1000 кубических сантиметров.
Высота бака цилиндрической формы равна 40 см, а площадь его основания 150 квадратных сантиметров. Чему равен объём этого бака (в литрах)? В одном литре 1000 кубических сантиметров.
Даны две кружки цилиндрической формы. Первая кружка вдвое выше второй, а вторая в четыре раза шире первой. Во сколько раз объём второй кружки больше объёма первой?
Ящик, имеющий форму куба с ребром 20 см без одной грани, нужно покрасить со всех сторон снаружи. Найдите площадь поверхности, которую необходимо покрасить. Ответ дайте в квадратных сантиметрах.
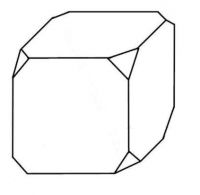
От деревянного кубика отпилили все его вершины (см.рис.). Сколько граней у получившегося многогранника(невидимые рёбра на рисунке не изображены)?
Бетонный шар весит 0,5 т. Сколько тонн будет весить шар вдвое большего радиуса, сделанный из такого же бетона?
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 20 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 20 см. Ответ дайте в кубических сантиметрах.
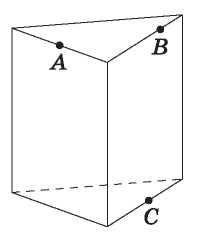
Плоскость, проходящая через точки A, B и C (см.рис.), разбивает правильную треугольную призму на два многогранника. Сколько вершин у получившегося многогранника с меньшим числом граней?
В сосуд цилиндрической формы налили воду до уровня 80 см. Какого уровня достигнет вода, если ее перелить в другой цилиндрический сосуд, у которого радиус основания в 4 раза больше, чем у первого? Ответ дайте в см.
