Задачи ЕГЭ профиль
- 1. Планиметрия
- 2. Векторы
- 3. Стереометрия
- 4. Классическое определение вероятности
- 5. Теория вероятностей
- 6. Уравнения
- 7. Нахождение значений выражений
- 8. Производная
- 9. Задачи прикладного содержания
- 10. Текстовые задачи
- 11. Графики функций
- 12. Исследование функций
- 13. Сложные уравнения
- 14. Стереометрия
- 15. Неравенства
- 16. Экономические задачи
- 17. Планиметрия
- 18. Параметры
- 19. Теория чисел
1. Планиметрия (Задачи ЕГЭ профиль)
Гипотенуза прямоугольного треугольника равна 28. Найдите радиус описанной окружности этого треугольника.
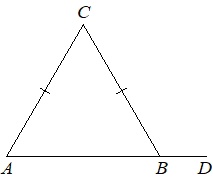
В треугольнике ABC стороны AC и BC равны. Внешний угол при вершине B равен 107°. Найдите угол C. Ответ дайте в градусах.
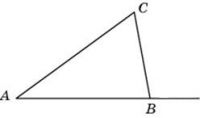
В треугольнике ABC угол A равен 14°, внешний угол при вершине B равен 91°. Найдите угол C. Ответ дайте в градусах.
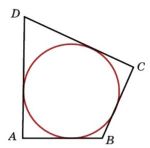
Угол A четырехугольника ABCD, вписанного в окружность, равен 25°. Найдите угол C четырехугольника. Ответ дайте в градусах.
В четырехугольник ABCD вписана окружность, AB=6, BC=4 и CD=16. Найдите четвертую сторону четырехугольника.
Найдите площадь прямоугольника, диагональ которого равна 5, а одна из сторон равна 4.
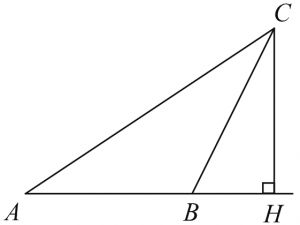
В треугольнике \(ABC\), изображенном на рисунке, угол \(A\) равен 30°, \(CH\) - высота, угол \(BCH\) равен 39°. Найдите угол \(ACB\). Ответ дайте в градусах.
Основания равнобедренной трапеции равны 6 и 12, а её периметр равен 28. Найдите площадь трапеции.
Периметр прямоугольника равен 42, а площадь 98. Найдите большую сторону прямоугольника.