24. Геометрические задачи на доказательство (Задачи ОГЭ)

В окруж­но­сти через се­ре­ди­ну O хорды AC про­ве­де­на хорда BD так, что дуги AB и CD равны. Докажите, что O — середина хорды BD.

Окружности с цен­тра­ми в точ­ках Aи Bпе­ре­се­ка­ют­ся в точ­ках C и D, причём точки Aи Bлежат по одну сто­ро­ну от пря­мой CD. Докажите, что CD ⊥ AB.

Докажите, что медиана треугольника делит его на два треугольника, площади которых равны.

В параллелограмме \(ABCD\) точка \(E\) - середина стороны \(AB\). Известно, что \(EC = ED\). Докажите, что данный параллелограмм - прямоугольник.

Известно, что около четырёхугольника ABCD можно описать окружность, и что продолжения сторон AD и BC пересекаются в точке K. Докажите, что треугольники KAB и KCD подобны.

В тре­уголь­ни­ке \(ABC\) с тупым углом \(ACB\) про­ве­де­ны вы­со­ты \(AA_1\) и \(BB_1\). Докажите, что тре­уголь­ни­ки \(A_1CB_1\) и \(ACB\) подобны.

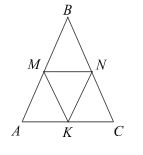
В равностороннем треугольнике \(ABC\) точки \(M\), \(N\), \(K\) — середины сторон \(АВ\), \(ВС\), \(СА\) соответственно. Докажите, что треугольник \(MNK\) — равносторонний.

На сред­ней линии тра­пе­ции ABCD с ос­но­ва­ни­я­ми AD и BC вы­бра­ли про­из­воль­ную точку F. Докажите, что сумма пло­ща­дей тре­уголь­ни­ков BFC и AFD равна по­ло­ви­не пло­ща­ди трапеции.

Окружности с центрами в точках \(I\) и \(J\) не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная у этим окружностям делит отрезок, соединяющий их центры, в отношении \(m:n\). Докажите, что диаметры этих окружностей относятся как \(m:n\).

Окружности с центрами в точках P иQ не имеют общих точек. Внутрення общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении a : b. Докажите, что диаметры этих окружностей относятся как a : b.