Задачи ЕГЭ база
Даны два конуса. Радиус основания и высота первого конуса равны, соответственно, 3 и 4, а второго - 6 и 6.
Во сколько раз объём второго конуса больше объёма первого?
Даны два цилиндра.Радиус основания и высота первого равны 2 и 3 соответственно, а второго 5 и 12. Во сколько раз площадь боковой поверхности второго цилиндра больше площади боковой поверхности первого?
Даны две кружки цилиндрической формы. Первая кружка вдвое выше второй, а вторая в четыре раза шире первой. Во сколько раз объём второй кружки больше объёма первой?
Две кружки имеют форму цилиндра. Первая кружка в полтора раза ниже второй, а вторая втрое уже первой. Во сколько раз объём первой кружки больше объёма второй?
Объём конуса равен \(9\pi\), а радиус его основания равен 3. Найдите высоту конуса.
Вода в сосуде цилиндрической формы находится на уровне \(h=80 см\). На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у данного? Ответ дайте в сантиметрах.
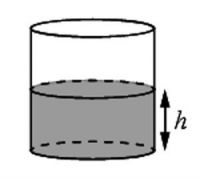
Вода в сосуде цилиндрической формы находится на уровне \(h=50 см\). На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания в два с половиной раза больше, чем у данного? Ответ дайте в сантиметрах.
Даны два конуса. Радиус основания и высота первого конуса равны соответственно 4 и 9, а второго – 6 и 8. Во сколько раз объём второго конуса больше объёма первого?
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен \(10\sqrt{2}\). Найдите образующую конуса.
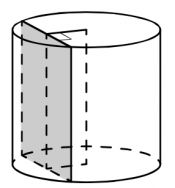
Радиус основания цилиндра равен 13, а его образующая равна 18. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 12. Найдите площадь этого сечения.
