На рисунке изображены графики функций \(f(x)=\dfrac{k}{x}\) и \(g(x)=ax+b\), которые пересекаются в точках А и В. Найдите ординату точки В.
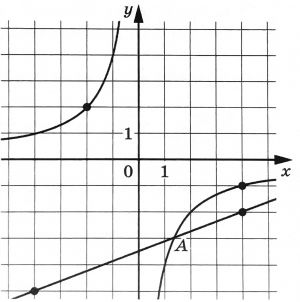

На рисунке изображены графики функций \(f(x)=\dfrac{k}{x}\) и \(g(x)=ax+b\), которые пересекаются в точках А и В. Найдите ординату точки В.

Так как там решений вообще не было, то пусть будет хоть какое-то. На счёт того, что b=-3,5 лучше так не рисковать и не быть уверенным, что это действительно так потому что это значение не лежит на узлах клеток и лучше найти его подставив известное нам значение х и а(которое в свою очередь является коэфицентом прямой), но я решил всё таки предположить, что это так и ускорить для себя процесс.
Сначала я нашёл нужный нам x, то есть 8 (не 4/3 так как этот х относится к точке А(ещё одно подтверждение правильного результата)). А затем я этот x подставил в одну из функций и нашел ординату, то есть y, который равен -0,5
Извините, что плохо расписал, но как получилось.



Про b=-3,5. Это действительно можно понять без подстановки. Из симметрии. Выделенные точки на прямой симметричны относительно вертикальной оси (на 4 левее и на 4 правее). Значит и пересечение прямой с вертикальной осью будет ровно посередине между ординатами этих точек. Между ними по вертикали 3 клетки. Значит, пересечение будет на 1,5 выше нижней и на 1,5 ниже верхней. А это как раз -3,5
Всего задач в тесте: 0
Вы ответили верно на: 0 (0 %)
Вы ответили неверно на: 0
Ваш первичный балл: 0
Ваш тестовый балл: 0