Задачи ЕГЭ база
- 1. Простые текстовые задачи
- 2. Величины и значения
- 3. Графики, диаграммы, таблицы
- 4. Вычисления по формуле
- 5. Теория вероятностей
- 6. Выбор подходящих вариантов
- 7. Функции и производные
- 8. Выбор утверждений
- 9. Фигуры на квадратной решетке. Координатная плоскость
- 10. Прикладные задачи по планиметрии
- 11. Прикладные задачи по стереометрии
- 12. Планиметрия
- 13. Стереометрия
- 14. Вычисления с дробями
- 15. Проценты и пропорции
- 16. Значения выражений
- 17. Уравнения
- 18. Неравенства и числовая прямая
- 19. Свойства чисел
- 20. Текстовые задачи
- 21. Нестандартные задачи
13. Стереометрия (Задачи ЕГЭ база)
Объем первого цилиндра равен 12 м³. У второго цилиндра высота в три раза больше, а радиус основания – в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 4, а боковое ребро \(\sqrt{17}\)
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4 и 2, а объём параллелепипеда равен 56. Найдите площадь поверхности этого параллелепипеда.
Найдите высоту правильной четырёхугольной пирамиды, сторона основания которой равна 2, а боковое ребро \(\sqrt{11}\)
В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 3, а гипотенуза равна √34. Найдите объём призмы, если её высота равна 6.
Даны два цилиндра. Радиус основания и высота первого равны 2 и 3 соответственно, а второго 5 и 12. Во сколько раз площадь боковой поверхности второго цилиндра больше площади боковой поверхности первого?
Два ребра прямоугольного параллелепипеда равны 12 и 5, а объем параллелепипеда равен 480. Найдите площадь поверхности этого параллелепипеда.
Конус имеет высоту, равную 16 см, и образующую, равную 20 см. Найдите объем конуса в см³, в ответе укажите объем, деленный на π.
Радиус основания цилиндра равен 13, а его образующая равна 18. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 12. Найдите площадь этого сечения.
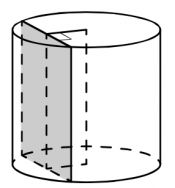
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.