Задачи ОГЭ
- 1. Практическая задача 1-5
- 2. См. раздел 1
- 3. См. раздел 1
- 4. См. раздел 1
- 5. См. раздел 1
- 6. Вычисления с дробями
- 7. Координатная прямая. Числовые неравенства
- 8. Степени и корни
- 9. Уравнения
- 10. Теория вероятностей
- 11. Функции и графики
- 12. Расчеты по формулам
- 13. Неравенства
- 14. Прогрессии
- 15. Треугольники
- 16. Окружности
- 17. Четырехугольники и многоугольники
- 18. Фигуры на клетчатой бумаге
- 19. Анализ геометрических утверждений
- 20. Уравнения, выражения, неравенства
- 21. Сложные текстовые задачи
- 22. Построение графиков
- 23. Геометрические задачи на вычисление
- 24. Геометрические задачи на доказательство
- 25. Сложные геометрические задачи
16. Окружности (Задачи ОГЭ)
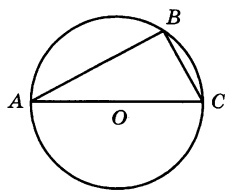
Сторона \(AC\) треугольника \(ABC\) проходит через центр описанной около него окружности. Найдите \(\angle{C}\), если \(\angle{A}=44^{\circ}\). Ответ дайте в градусах.
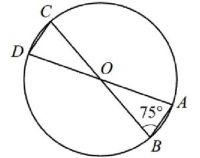
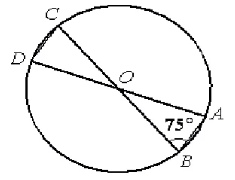
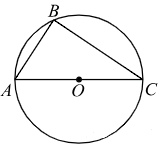
В окружности с центром в точке \(O\) проведены диаметры \(AD\) и \(BC\), угол \(ABO\) равен 75°. Найдите величину угла \(ODC\).
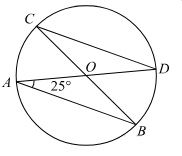
В окружности с центром в точке \(O\) проведены диаметры \(AD\) и \(BC\), угол \(OAB\) равен 25°. Найдите величину угла \(OCD\).
В окружности с центром в точке O проведены диаметры AD и BC, угол ABO равен 75°. Найдите величину угла ODC.
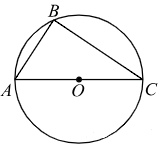
Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A = 75°. Ответ дайте в градусах.
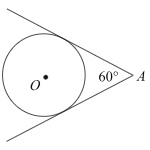
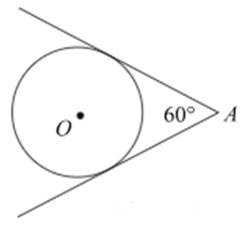
Из точки \(A\) проведены две касательные к окружности с центром в точке \(O\). Найдите радиус окружности, если угол между касательными равен 60, а расстояние от точки \(A\) до точки \(O\) равно 8.
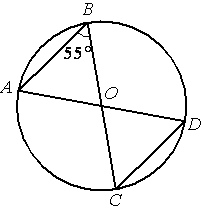
В окружности с центром в точке O проведены диаметры AD и BC, угол ABO равен 55°. Найдите величину угла ODC.
Центр окружности, описанной около треугольника \(ABC\), лежит на стороне \(AB\). Найдите угол \(ABC\), если угол \(BAC\) равен 75°. Ответ дайте в градусах.
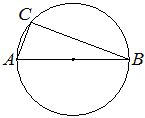
Сторона \(AC\) треугольника \(ABC\) проходит через центр описанной около него окружности. Найдите \(\angle{C}\), если \(\angle{A} = 44°\). Ответ дайте в градусах.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.