Задачи ОГЭ
- 1. Практическая задача 1-5
- 2. См. раздел 1
- 3. См. раздел 1
- 4. См. раздел 1
- 5. См. раздел 1
- 6. Вычисления с дробями
- 7. Координатная прямая. Числовые неравенства
- 8. Степени и корни
- 9. Уравнения
- 10. Теория вероятностей
- 11. Функции и графики
- 12. Расчеты по формулам
- 13. Неравенства
- 14. Прогрессии
- 15. Треугольники
- 16. Окружности
- 17. Четырехугольники и многоугольники
- 18. Фигуры на клетчатой бумаге
- 19. Анализ геометрических утверждений
- 20. Уравнения, выражения, неравенства
- 21. Сложные текстовые задачи
- 22. Построение графиков
- 23. Геометрические задачи на вычисление
- 24. Геометрические задачи на доказательство
- 25. Сложные геометрические задачи
16.2. Радиусы, хорды, касательные, секущие (Задачи ОГЭ)
Из точки \(A\) проведены две касательные к окружности с центром в точке \(O\). Найдите радиус окружности, если угол между касательными равен 60, а расстояние от точки \(A\) до точки \(O\) равно 8.
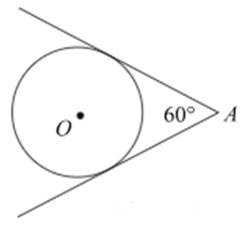
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
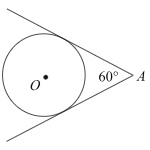
Из точки \(А\) проведены две касательные к окружности с центром в точке \(О\). Найдите радиус окружности, если угол между касательными равен \(60^{\circ}\), а расстояние от точки \(А\) до точки \(О\) равно \(6\).
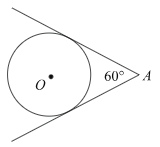
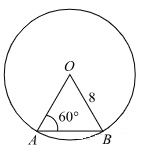
Центральный угол \(AOB\) опирается на хорду \(AB\) так, что угол \(OAB\) равен \(60^{\circ}\). Найдите длину хорды \(AB\), если радиус окружности равен \(8\).
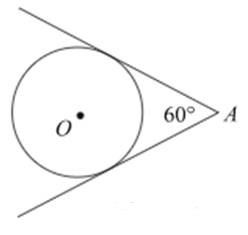
Из точки \(A\) проведены две касательные к окружности с центром в точке \(O\). Найдите радиус окружности, если угол между касательными равен 60, а расстояние от точки \(A\) до точки \(O\) равно 6.
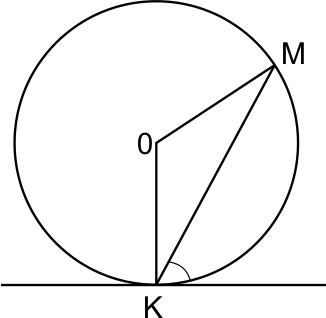
Прямая касается окружности в точке \(K\). Точка \(O\) - центр окружности. Хорда \(KM\) образует с касательной угол, равный 83°. Найдите величину угла \(OMK\). Ответ дайте в градусах.
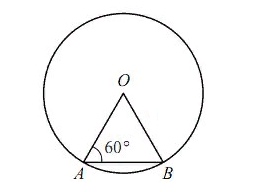
Центральный угол \(AOB\) опирается на хорду \(AB\) так, что угол \(OAB\) равен 60°. Найдите длину хорды \(AB\), если радиус окружности равен 8.
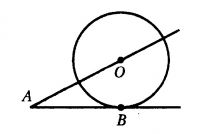
К окружности с центром в точке \(O\) проведены касательная \(AB\) и секущая \(AO\). Найдите радиус окружности, если \(AB = 12\), \(AO = 13\).
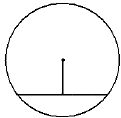
Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см. Ответ дайте в см.
К окружности с центром в точке \(О\) проведены касательная \(AB\) и секущая \(AO\). Найдите радиус окружности, если \(AB = 14\) см, \(AO = 50\) см.