Задачи ОГЭ
- 1. Практическая задача 1-5
- 2. См. раздел 1
- 3. См. раздел 1
- 4. См. раздел 1
- 5. См. раздел 1
- 6. Вычисления с дробями
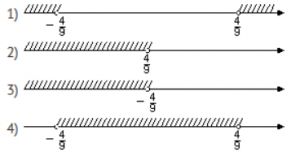
- 7. Координатная прямая. Числовые неравенства
- 8. Степени и корни
- 9. Уравнения
- 10. Теория вероятностей
- 11. Функции и графики
- 12. Расчеты по формулам
- 13. Неравенства
- 14. Прогрессии
- 15. Треугольники
- 16. Окружности
- 17. Четырехугольники и многоугольники
- 18. Фигуры на клетчатой бумаге
- 19. Анализ геометрических утверждений
- 20. Уравнения, выражения, неравенства
- 21. Сложные текстовые задачи
- 22. Построение графиков
- 23. Геометрические задачи на вычисление
- 24. Геометрические задачи на доказательство
- 25. Сложные геометрические задачи
13.2. Квадратные неравенства (Задачи ОГЭ)
Множеством решений какого неравенства является следующее множество значений переменной \(x\)?
\(x\in[-5;5]\)
1) \(x^2-25\leqslant 0\)
2) \(x^2-25>0\)
3) \(x^2+25< 0\)
4) \(x-5\geqslant 0\)
Укажите неравество, которое не имеет решение.
1) \(x^{2}+78>0\)
2) \(x^{2}+78<0\)
3) \(x^{2}-78>0\)
4) \(x^{2}-78<0\)
Укажите решение неравенства \(x^2-49<0\).
1) нет решений
2) \((-\infty;+\infty)\)
3) \((-7;7)\)
4) \((-\infty;-7)\cup(7;+\infty)\)
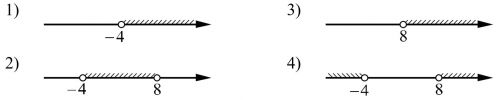
Укажите решение неравенства \((x+2)(x-7)\leqslant 0\).
1) \([-2; 7]\)
2) \((-\infty; -2] \cup [7; +\infty)\)
3) \((-\infty; 7]\)
4) \((-\infty; -2]\)
Решите неравенство \(x^2 + 2x \geqslant 0\). В ответ укажите номер правильного варианта.
1) \((-\infty;-2]\cup[0;+\infty)\)
2) \([-2;0]\)
3) \([0;2]\)
4) \((-\infty;0]\cup[2;+\infty)\)
Найдите количество целых чисел, являющихся решениями неравенства \({-x^2+15x-54}\geqslant 0 \).