9. Производная (Задачи ЕГЭ профиль)

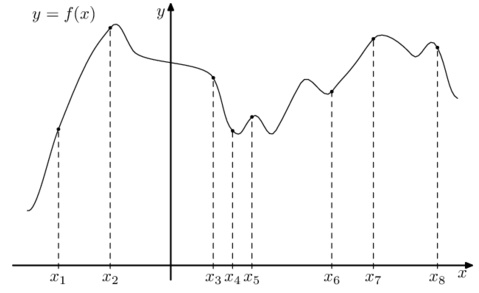
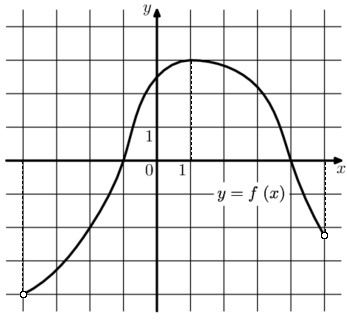
На рисунке изображён график дифференцируемой функции \(y=f(x)\), определённой на интервале \((-4;5)\). Найдите точку из отрезка \([-2;4]\), в которой производная функции \(f(x)\) равна 0.

На рисунке изображен график функции \(y=f(x)\), определенной на интервале (-3;9). Определите количество точек, в которых производная функции \(f(x)\) равна 0.

На рисунке изображён график функции y=f(x). На оси абсцисс отмечены десять точек: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀. Найдите количество точек, в которых производная функции f(x) положительна.

​

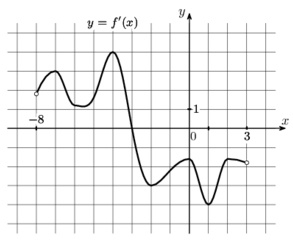
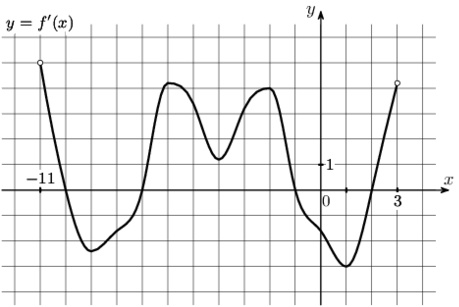
На рисунке изображен график \(y=f'(x)\) – производной функции \(f(x)\), определенной на интервале (-11;3). Найдите промежутки возрастания функции \(f(x)\). В ответ укажите длину наибольшего из них.

На рисунке изображен график y=f'(x) – производной функции y=f(x), определенной на интервале (-8;3). Найдите точку экстремума функции y=f(x), принадлежащую отрезку [-6;1].

На рисунке изображен график функции y=f’(x) - производной функции y=f(x) и одиннадцать точек на оси абсцисс: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁. Сколько из этих точек принадлежит промежуткам убывания функции f(x)?

​

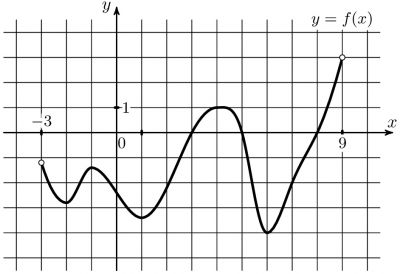
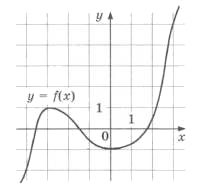
На рисунке изображен график функции \(y = f(x)\). Найдите точку, в которой функция \(f(x)\) принимает наибольшее значение на отрезке \([-4; 3]\).

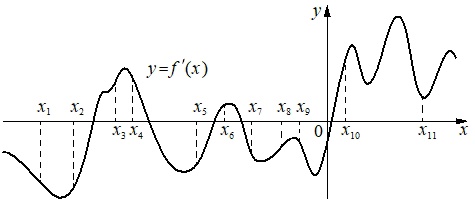
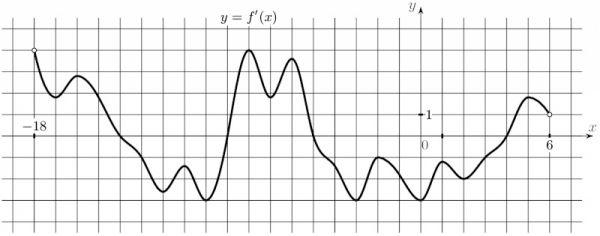
На рисунке изображен график производной функции \(y=f(x)\), определенной на интервале (-18;6). Найдите длину наибольшего промежутка убывания этой функции.

Материальная точка движется прямолинейно по закону \(x(t)=6t^2-48t+17  \), где \(x\) - расстояние от точки отсчёта в метрах, \(t\) - время в секундах, прошедшее с начала движения. Найдите её скорость (в метрах в секунду) в момент времени \(t=9\) с

На рисунке изображён график функции \(y=f'(x)\) - производной функции \(f(x)\), определённой на интервале \((-3 ; 8)\) . Найдите точку минимума функции\(f(x)\) .