Задачи ЕГЭ профиль
- 1. Планиметрия
- 2. Векторы
- 3. Стереометрия
- 4. Классическое определение вероятности
- 5. Теория вероятностей
- 6. Уравнения
- 7. Нахождение значений выражений
- 8. Производная
- 9. Задачи прикладного содержания
- 10. Текстовые задачи
- 11. Графики функций
- 12. Исследование функций
- 13. Сложные уравнения
- 14. Стереометрия
- 15. Неравенства
- 16. Экономические задачи
- 17. Планиметрия
- 18. Параметры
- 19. Теория чисел
3.1. Многогранники (Задачи ЕГЭ профиль)
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
Найдите объем прямоугольного параллелепипеда, ребра которого равны 3, 5, 6.
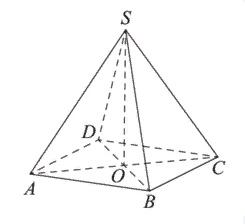
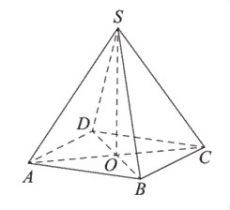
В правильной четырехугольной пирамиде SABCD точка O - центр основания, S - вершина, SA=10, BD=16. Найдите длину отрезка SO.
Во сколько раз увеличится объем пирамиды, если её высоту увеличить в четыре раза?
В правильной четырехугольной пирамиде SABCD с вершиной S точка O - центр основания, SO=35, SD=37. Найдите длину отрезка BD.
В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известно, что AB=7, BC=6, AA₁=5. Найдите объём многогранника, вершинами которого являются точки A, B, C, A₁, B₁, C₁.
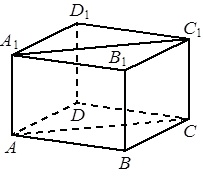
В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известно, что BB₁=16, A₁B₁=2, A₁D₁=8. Найдите длину диагонали AC₁.
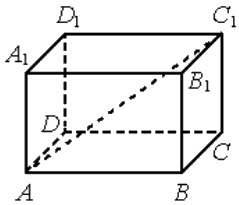
В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ рёбра DA, DC и диагональ DA₁ боковой грани равны соответственно 3, 5 и √34. Найдите объём параллелепипеда ABCDA₁B₁C₁D₁.
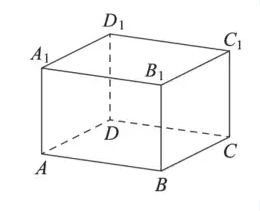
Диагональ правильной четырехугольной призмы наклонена к плоскости основания под углом 30°. Боковое ребро равно 3. Найдите диагональ призмы.
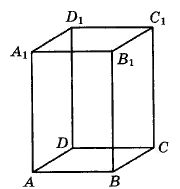
Через среднюю линию основания правильной треугольной призмы, объём которой равен 84, проведена плоскость, параллельная боковому ребру. Найдите объём отсечённой треугольной призмы.