Задачи ЕГЭ профиль
- 1. Планиметрия
- 2. Векторы
- 3. Стереометрия
- 4. Классическое определение вероятности
- 5. Теория вероятностей
- 6. Уравнения
- 7. Нахождение значений выражений
- 8. Производная
- 9. Задачи прикладного содержания
- 10. Текстовые задачи
- 11. Графики функций
- 12. Исследование функций
- 13. Сложные уравнения
- 14. Стереометрия
- 15. Неравенства
- 16. Экономические задачи
- 17. Планиметрия
- 18. Параметры
- 19. Теория чисел
1.3. Окружности (Задачи ЕГЭ профиль)
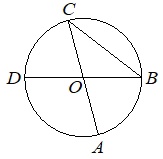
Отрезки AC и BD - диаметры окружности с центром O. Угол AOD равен 130°. Найдите вписанный угол ACB. Ответ дайте в градусах.
Гипотенуза прямоугольного треугольника равна 28. Найдите радиус описанной окружности этого треугольника.
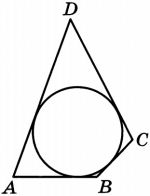
В четырехугольник ABCD вписана окружность, AB=10, CD=17. Найдите периметр четырехугольника ABCD.
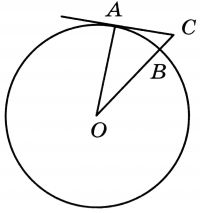
Угол ACO равен 62°. Его сторона CA касается окружности с центром в точке O. Отрезок CO пересекает окружность в точке B (см. рис.). Найдите градусную меру дуги AB окружности, заключённой внутри этого угла. Ответ дайте в градусах.
Треугольник ABC вписан в окружность с центром O. Угол BAC равен 25°. Найдите угол BOC. Ответ дайте в градусах.
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 5?
Найдите вписанный угол, опирающийся на дугу, длина которой равна 1/5 длины окружности. Ответ дайте в градусах.
Точки A, B и С, расположенные на окружности, делят ее на три дуги, градусные меры которых относятся как 1:8:9. Найдите больший угол треугольника ABC. Ответ дайте в градусах.
Отрезки AC и BD – диаметры окружности с центром O. Угол ACB равен 41°. Найдите величину угла AOD. Ответ дайте в градусах.

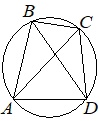
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 120°, угол ABD равен 43°. Найдите угол CAD. Ответ дайте в градусах.