Набор №548

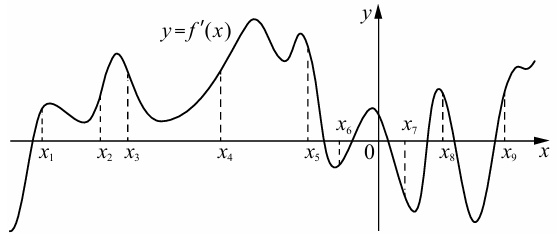
На рисунке изображен график функции y=f’(x) - производной функции y=f(x) и одиннадцать точек на оси абсцисс: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁. Сколько из этих точек принадлежит промежуткам убывания функции f(x)?

​

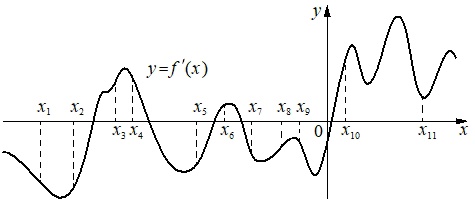
На рисунке изображён график \(y=f'(x)\) – производной функции \(f(x)\). На оси абсцисс отмечено девять точек: \(x_1, x_2, ..., x_9\). Сколько из этих точек принадлежат промежуткам убывания функции \(f(x)\)?

​

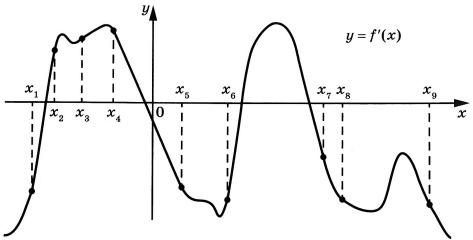
На рисунке изображён график \(y=f'(x)\) – производной функции \(f(x)\). На оси абсцисс отмечены девять точек: \(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}, x_{7}, x_{8}, x_{9}\). Сколько из этих точек лежит на промежутках убывания функции \(f(x)\)?

На рисунке показан график \(y=f'(x)\) производной функции \(y=f(x)\). На оси абцисс отмечены шесть точек: \(x_1,x_2,x_3,x_4,x_5,x_6\). Сколько из этих точек лежит на промежутках убывания функции \(y=f(x)\)?

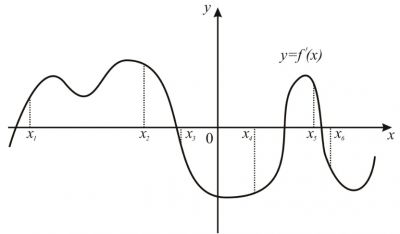
На рисунке изображён график \(y=f'(x)\) - производной функции \(f(x)\). На оси абсцисс отмечены 10 точек: \(x_1\), \(x_2\), \(x_3\), \(x_4\), \(x_5\), \(x_6\), \(x_7\), \(x_8\), \(x_9\), \(x_{10}\). Сколько из этих точек лежит на промежутках убывания функции \(f(x)\)?

​

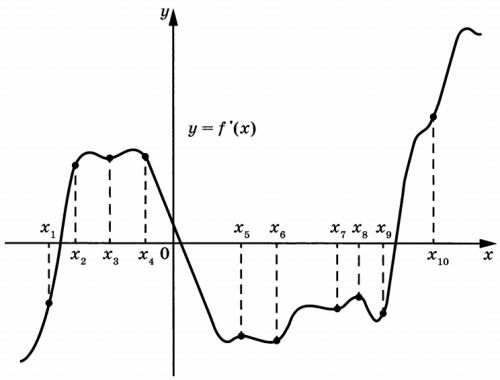
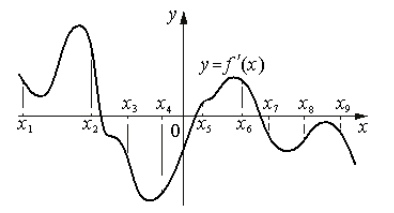
На рисунке изображен график функции y = f'(x) - производной функции f(x). На оси абсцисс отмечено семь точек: x₁, x₂, x₃, x₄, x₅, x₆, x₇. Сколько из этих точек принадлежит промежуткам убывания функции f(x)?

​

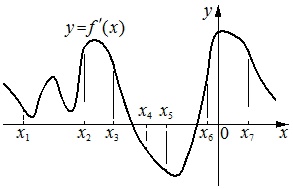
На рисунке изображён график \(y=f'(x)\) – производной функции \(f(x)\). На оси абсцисс отмечено девять точек: \(x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8, x_9\). Сколько из этих точек принадлежат промежуткам убывания функции \(f(x)\)?

​