#2293: Решение задачи через вычисление коэффициента b

Условие

На рисунке изображен график функции \(f(x)=2x^2+bx+c\), где числа \(b\) и \(c\) – целые. Найдите \(f(-5)\).

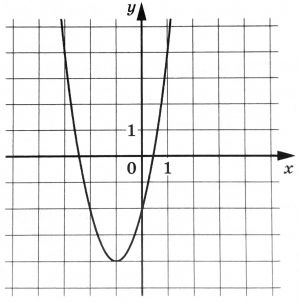
картинка

Добрый день!
Суть обсуждения:
Давайте попробуем вычислить коэфицент b по формуле x0 = -b/2a => 1 = b/4 => b = 4

По графику видно, что коэффициент с = -4. Подставим в функцию:

f(x) = 2*x^2 + 4*x - 4
f(-5) = 2 * 25 - 20 - 4 = 50 - 24 = 26.

По какой причине возникает расхождение с ответом?

С уважением,
Аркадий

Ответы (5)

Почему у тебя с=-4?

Дмитрий Создатель,

Разве коэф. с не отвечает за смещение вершины пораболы относительно Oy?

Верный ответ

Аркадий Пронин, ты, кажется, путаешь вид записи квадратичной функции \(f(x)=a(x-x_в)^2+y_в\) и \(f(x)=ax^2+bx+c\).

В первом \(y_в\) - это абсцисса вершины, а вот во втором \(c=f(0)\) - ордината точки пересечения с вертикальной осью. На этом рисунке с=-2

Дмитрий Создатель,

Вот оно что. Спасибо большое!

с=-2

Возьми две точки (-1;4) (0;-2)

Составляем уравнение с=-2 и 2-b+c=-4

Решаем и получаем b=4

Теперь возращаемся к функции F(-5)=25*2-4*5-2=28

Загрузка...