На рисунке изображён график функции \(f(x)=a^{x+b}\). Найдите \(f(-3)\)
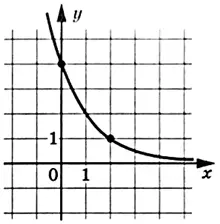

На рисунке изображён график функции \(f(x)=a^{x+b}\). Найдите \(f(-3)\)

Как решить

Подставить координты двух точек, чтобы получить систему уравнений и найти из неё \(a\) и \(b\):
\(\begin{cases}f(0)=a^{0+b}=4\\f(2)=a^{2+b}=1\end{cases}\)
\(\begin{cases}a^{b}=4\\2+b=0\end{cases}\)
\(\begin{cases}a^{-2}=4\\b=-2\end{cases}\)
\(\begin{cases}a^{-2}=4\\b=-2\end{cases}\)
\(\begin{cases}a^{2}=\dfrac14\\b=-2\end{cases}\)
\(\begin{cases}a=\dfrac12\\b=-2\end{cases}\)
Получили, что \(f(x)=\left(\dfrac12\right)^{x-2}\)
Оставлось подставить \(x=-3\):
\(f(-3)=\left(\dfrac12\right)^{-3-2}=\left(\dfrac12\right)^{-5}=2^5=32\)

Артак Саргсян,
Берём две точки, через которые проходит график, так как нам не известны два параметра a и b. Это точки с координатами (2;1) и (0;4). Подставляем в формулу вместо x сначала 2, вместо y - 1. Получим одно уравнение. Потом подставляем координаты второй точки, вместо x - 0, вместо y - 4. И решаем систему из этих двух уравнений. Оттуда найдём а и b, а уже потом, когда получим формулу показательной функции, вместо x берём - 3 и находим чему равен y.

Артак Саргсян,
Можно решить вторым способом, через сдвиги и переносы графика вдоль осей. График обычной показательной проходит через точку (0;1), наш проходит через точку (2;1), то есть сдвинут вдоль оси Х вправо на 2 единицы, значит, b равно - 2. А потом подставить одну точку и найти а. А дальше по той же схеме.
Всего задач в тесте: 0
Вы ответили верно на: 0 (0 %)
Вы ответили неверно на: 0
Ваш первичный балл: 0
Ваш тестовый балл: 0
