#3734: Точка 2

Условие

На рисунке изображён график функции \(y=f(x)\). На оси абсцисс отмечены точки -1, 1, 2, 3. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

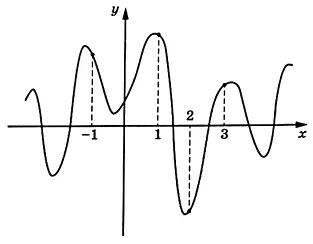
картинка

Я так понял что подходит точка 2 потому что функция убывала(изменялась) на участке до этой точки значительно быстрее чем перед другими. Или по другой причине?

Ответы (2)

Во-первых мы смотрим на движение функции слева - направо. Далее проводим небольшие отрезки касательных в каждой из названных точек. Там, где функция убывает, касательная, если ее продолжить, образует с обсью Ох тупой угол (это точки -1 и 1), а там где функция возрастает (точки 2 и 3), касательная образует острый угол с осью Ох. Тангенс тупого угла - отрицательный и, соответственно, производная в такой точке - отрицательная. Тангенс острого угла положительный, следовательно, производная положительная, причем чем больше острый угол, тем больше тангенс наклона касательной, тем больше производная. Чем круче вниз идет касательгная - тем меньше производная (отрицательная), чем круче вверх идет касательная - тем больше производная (положительная). В точке 2 касательная круче, чем в точке 3. Ответ: точка 2. (Хотя в этих двух точках различие незначительное, могли бы поставить точку 2 чуть правее.)

Значение производной в точке равно углу наклона касательной. в точке 2 коэффициент наклона прямой наибольший.

Загрузка...