На рисунке изображен график \(y=f'(x)\) – производной функции \(y=f(x)\), определенной на интервале (-9;3). Найдите количество точек, в которых касательная к графику функции \(y=f(x)\) параллельна прямой \(y=2x-23\) или совпадает с ней.
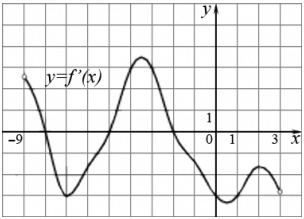

На рисунке изображен график \(y=f'(x)\) – производной функции \(y=f(x)\), определенной на интервале (-9;3). Найдите количество точек, в которых касательная к графику функции \(y=f(x)\) параллельна прямой \(y=2x-23\) или совпадает с ней.

Почему спрашивается: "Параллельна или совпадает ", а ответ идёт только на совпадает с точкой 2?

Ответ 5. Пересчитайте точки.

Параллельные прямые имеют одинаковый угловой коэффициент, то есть одинаковый тангенс угла наклона к положительному направлению оси Ох. Для решения задачи нам важно только значение этого коэффициента: к=2. Поэтому и говорится о всех прямых, имеющих такой коэффициет: о касательной и параллельных ей прямых. Откуда мы получаем значение производной 2. По графику производной видно, что значение 2 она принимает 3 раза. Ответ 3.

Параллельные прямые характеризуются тем, что у них равны коээфициенты угла наклона прямой. У прямой y=2x-23 угол наклона k=2, он же равен тангенсу угла наклона, и так же значению производной. Дан график именно производной, поэтому теперь тебе просто нужно найти количество раз, когда производная f ' (x) = 2. На рисунке таких точек 3.

В ответ идут и те точки,в которых касательная и параллельна, и те,в которых касательная совпадает с прямой,описываемой данным уравнением.речь о точках графиках функции и их касательных.Известно,что у параллельных прямых одиннаковые параметры К,(у=кх+в), а на графике производной,это как раз и будут точки с абсциссами равными х=к,так как у'=к.

Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой y=2x−23 или совпадает с ней, их угловые коэффициенты равны 2. Найдем количество точек, в которых f′(x)y = 2 это соответствует количеству точек пересечения графика производной с прямой y = 2. На данном интервале таких точек 3.

Если стало понятно, то отметь какой-то ответ как верный, чтобы вопрос стал закрыт
Всего задач в тесте: 0
Вы ответили верно на: 0 (0 %)
Вы ответили неверно на: 0
Ваш первичный балл: 0
Ваш тестовый балл: 0
