Математика 5 класс
Меню курса
Законы сложения
Переместительный закон сложения
Заметим, что если не к числу 6 прибавить 3, а наоборот к числу 3 прибавить число 6, то результат получится тем же — 9:

6+3=3+6=9
Это верно для суммы любых двух чисел, ведь сумма содержит столько единиц, сколько было во всех слагаемых вместе. Поэтому, не важно, в каком порядке их записывать, результат (общее количество единиц) от этого не поменяется.
Это свойство называют переместительным законом сложения:
От перестановки слагаемых сумма не меняется.
То есть, для любых натуральных чисел \(a\) и \(b\) верно равенство: \(a+b=b+a\)
Сочетательный закон сложения
Складывать можно не только два, но и больше натуральных чисел. Для примера, найдем сумму чисел 3, 4 и 2. Сделаем это последовательно – сложим сначала первые два числа, а потом к их сумме прибавим третье. Это записывается следующим образом: (3+4)+2. Скобки здесь нужны для того, чтобы определить порядок действий. Сначала выполняется действие в скобках, а потом действие вне скобок. То есть, они показывают, что сперва мы складываем числа 3 и 4, которые внутри скобок, а потом к результату прибавляем число 2.
Отметим на координатном луче число 3 и сдвинемся от него вправо на 4 деления – получим число 7. Значит, 3+4=7. Теперь уже от числа 7 сдвинемся вправо на 2 деления – получим число 9. Следовательно, (3+4)+2=9.

А теперь сложим эти же числа, но в другом порядке. Сначала сложим 4 и 2, а потом эту сумму прибавим к 3.
4+2=6 (это отдельно на координатном луче изображать не будем). А вот теперь к числу 3 прибавим сумму 2 и 4, то есть 6. Это изобразим на координатном луче и снова окажемся в точке с координатой 9.
Записать такую последовательно действий тоже можно с помощью скобок: 3+(4+2)=9.
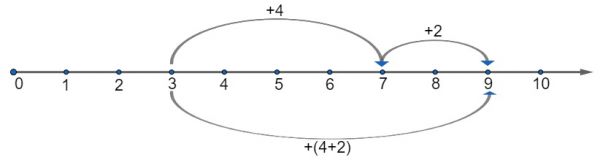
Таким образом, мы получили равенство (3+4)+2=3+(4+2). То же самое будет верно для суммы любых трёх чисел.
Это свойство называется сочетательный закон сложения:
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего числа.
То есть, для любых натуральных чисел \(a\), \(b\) и \(c\) верно равенство: \((a+b)+c=a+(b+c)\)
Вместо \((a+b)+c\) пишут короче \(a+b+c\). Когда в записи суммы нет скобок, то сложение выполняют по порядку слева направо.
Из этих двух законов следует, что при сложении нескольких чисел слагаемые можно менять местами и производить сложение в любом порядке (то есть, заключать слагаемые в скобки любым образом, чтобы поменять порядок вычислений). Например:
\((a+b)+(c+d)=a+(b+c)+d=(d+a+c)+b=c+b+(d+a)=d+c+a+b=a+b+c+d\)
Прибавление нуля
Рассмотрим отдельно сложение натурального числа и нуля (сам 0 натуральным числом не является).
Сумма двух чисел, одно из которых 0, равна второму числу.
То есть, для любого натурального \(a\) верны равенства: \(a+0=0+a=a\)
Если оба слагаемых нули, то сумма тоже равна 0.