Открытый банк ФИПИ
11. Графики функций
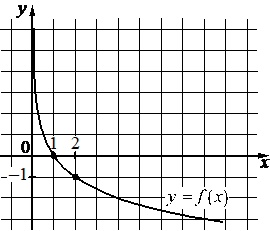
На рисунке изображён график функции вида \(f(x)=\log_ax\). Найдите значение \(f(8)\)
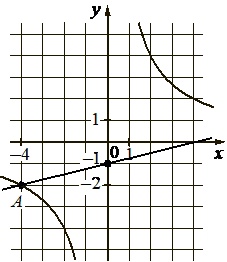
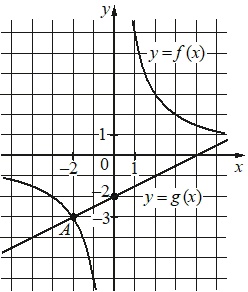
На рисунке изображены графики функций \(f(x)=\dfrac{k}{x}\) и \(g(x)=ax+b\), которые пересекаются в точках A и B. Найдите абсциссу точки B.
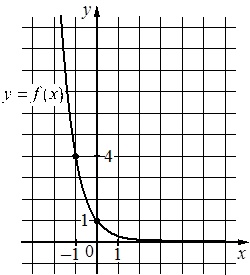
На рисунке изображен график функции \(f(x)=a^x\). Найдите \(f(-3)\)
На рисунке изображен график функции \(f(x)=ax^2+bx+c\). Найдите \(f(-2)\)
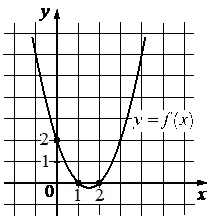
На рисунке изображен график функции \(f(x)=a^x\). Найдите \(f(-3)\)
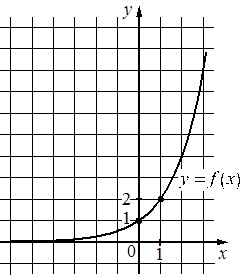
На рисунке изображен график функции вида \(f(x)=a^x\). Найдите значение \(f(-3)\)
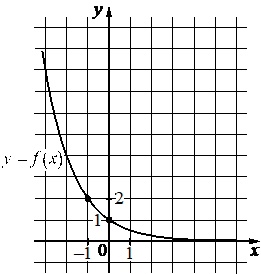
На рисунке изображен график функции \(f(x)=kx+b\). Найдите \(f(7)\)
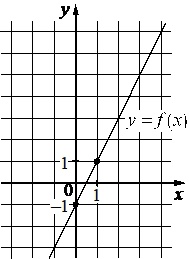
На рисунке изображён график функции вида \(f(x)=\log_ax\). Найдите значение \(f(8)\)
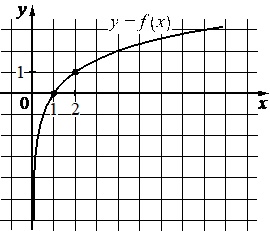
На рисунке изображены графики функций \(f(x)=a\sqrt{x}\) и \(g(x)=kx\), которые пересекаются в точках A и B. Найдите абсциссу точки B.
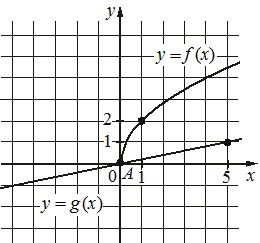
На рисунке изображены графики функций \(f(x)=ax^2+bx+c\) и \(g(x)=kx\), пересекающиеся в точках А и B. Найдите абсциссу точки B.
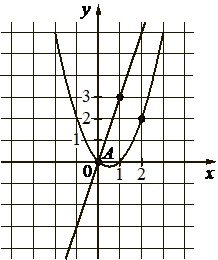
На рисунке изображен график функции вида \(f(x)=a^x\). Найдите значение \(f(2)\)
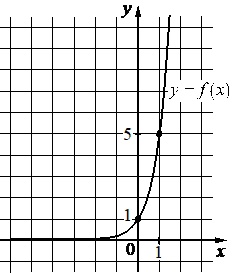
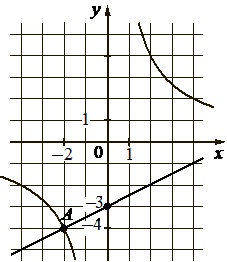
На рисунке изображены графики функций видов \(f(x)=\dfrac{k}{x}\) и \(g(x)=ax+b\), пересекающиеся в точках A и B. Найдите абсциссу точки B.
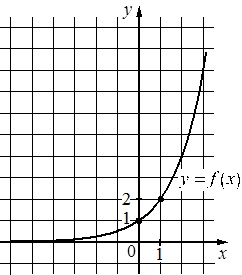
На рисунке изображен график функции вида \(f(x)=a^x\). Найдите \(f(4)\)
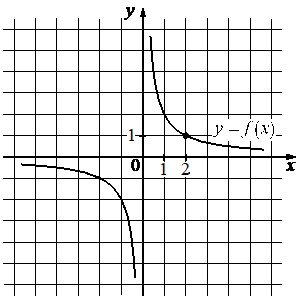
На рисунке изображен график функции вида \(f(x)=\dfrac{k}{x}\). Найдите значение \(f(10)\)
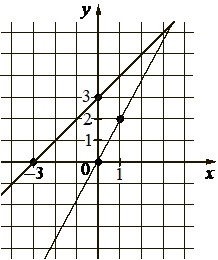
На рисунке изображены графики двух линейных функций, пересекающиеся в точке A. Найдите абсциссу точки A.
На рисунке изображен график функции \(f(x)=\log_ax\). Найдите \(f(25)\)

На рисунке изображен график функции \(f(x)=\dfrac{k}{x}\). Найдите \(f(10)\)
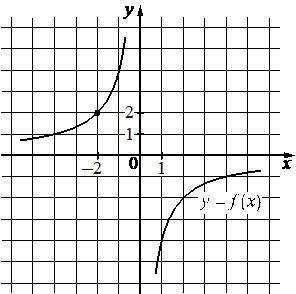
На рисунке изображены графики функций видов \(f(x)=\dfrac{k}{x}\) и \(g(x)=ax+b\), пересекающиеся в точках A и B. Найдите абсциссу точки B.
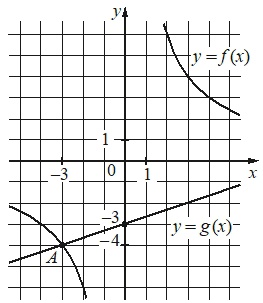
На рисунке изображен график функции вида \(f(x)=\dfrac{k}{x}\). Найдите \(f(20)\)
На рисунке изображены графики функций \(f(x)=ax^2+bx+c\) и \(g(x)=kx\), пересекающиеся в точках А и B. Найдите абсциссу точки B.
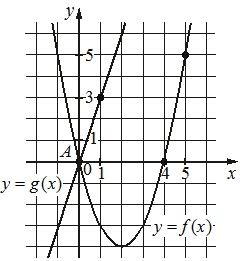
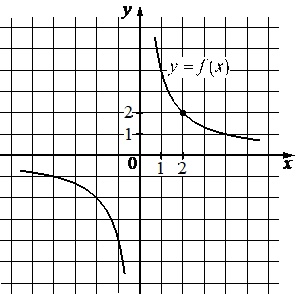
На рисунке изображен график функции \(f(x)=\dfrac{k}{x}\). Найдите \(f(10)\)
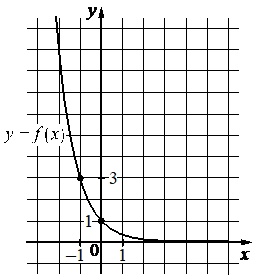
На рисунке изображен график функции \(f(x)=a^x\). Найдите \(f(-3)\)
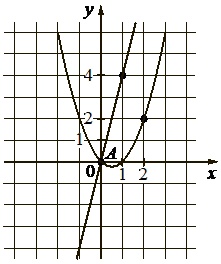
На рисунке изображены графики функций \(f(x)=ax^2+bx+c\) и \(g(x)=kx\), пересекающиеся в точках А и В. Найдите абcциссу точки В.
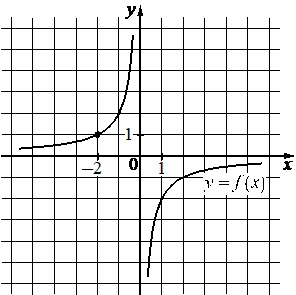
На рисунке изображены графики функций видов \(f(x)=\dfrac{k}{x}\) и \(g(x)=ax+b\), пересекающиеся в точках A и B. Найдите абсциссу точки B.
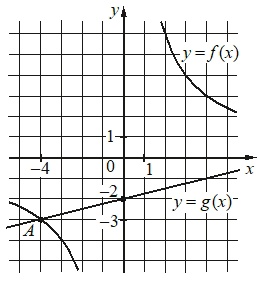
На рисунке изображены графики двух линейных функций, пересекающиеся в точке A. Найдите абсциссу точки A.
На рисунке изображены графики функций \(f(x)=ax^2+bx+c\) и \(g(x)=kx\), пересекающиеся в точках А и B. Найдите абсциссу точки B.
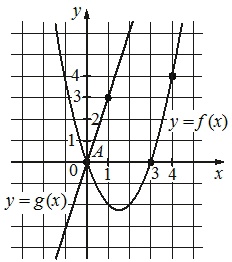
На рисунке изображен график функции вида \(f(x)=a^x\). Найдите \(f(3)\)
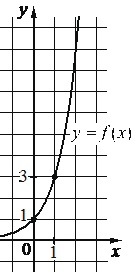
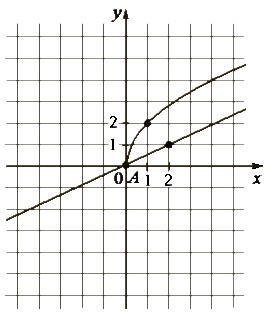
На рисунке изображены графики функций \(f(x)=a\sqrt{x}\) и \(g(x)=kx\), которые пересекаются в точках A и B. Найдите абсциссу точки B.
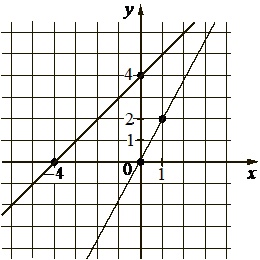
На рисунке изображен график функции вида \(f(x)=kx+b\). Найдите \(f(5)\)
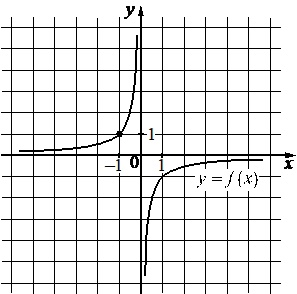
На рисунке изображен график функции вида \(f(x)=\dfrac{k}{x}\). Найдите значение \(f(10)\)
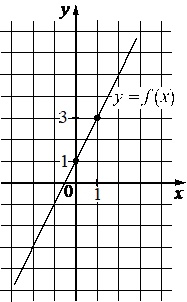
На рисунке изображен график функции вида \(f(x)=kx+b\). Найдите \(f(4)\)

На рисунке изображён график функции вида \(f(x)=\log_ax\). Найдите значение \(f(16)\)

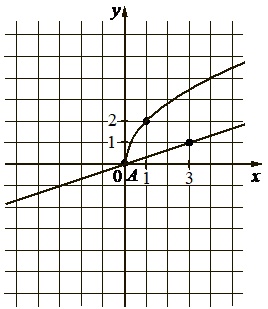
На рисунке изображены графики функций \(f(x)=a\sqrt{x}\) и \(g(x)=kx\), которые пересекаются в точках A и B. Найдите абсциссу точки B.
На рисунке изображен график функции \(f(x)=ax^2+bx+c\). Найдите \(f(-3)\)
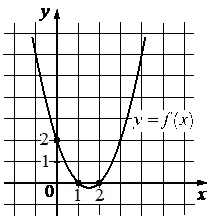
На рисунке изображен график функции \(f(x)=kx+b\). Найдите \(f(6)\)
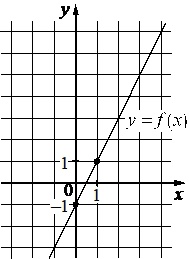
На рисунке изображён график функции вида \(f(x)=\log_ax\). Найдите значение \(f(32)\)

На рисунке изображены графики функций \(f(x)=a\sqrt{x}\) и \(g(x)=kx\), которые пересекаются в точках A и B. Найдите абсциссу точки B.
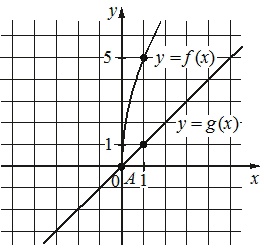
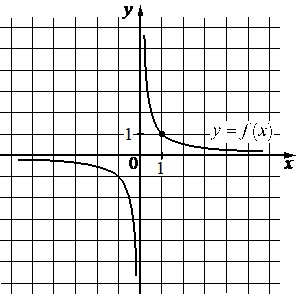
На рисунке изображен график функции вида \(f(x)=\dfrac{k}{x}\). Найдите значение \(f(10)\)
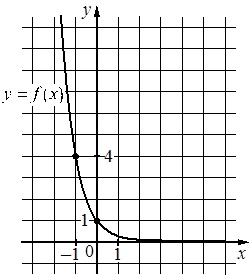
На рисунке изображен график функции вида \(f(x)=a^x\). Найдите значение \(f(-4)\)

На рисунке изображён график функции вида \(f(x)=\log_ax\). Найдите значение \(f(16)\)

На рисунке изображен график функции вида \(f(x)=a^x\). Найдите значение \(f(-2)\)
На рисунке изображены графики функций видов \(f(x)=\dfrac{k}{x}\) и \(g(x)=ax+b\), пересекающихся в точках A и B. Найдите абсциссу точки B.
На рисунке изображен график функции вида \(f(x)=\dfrac{k}{x}\). Найдите значение \(f(30)\)