2. Векторы

Даны векторы \(\vec{a}(25;0)\) и \(\vec{b}(1;-5)\). Найдите длину вектора \(\vec{a}-4\vec{b}\)

Даны векторы \(\vec{a}(-13;4)\) и \(\vec{b}(-6;1)\). Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)

Даны векторы \(\vec{a}(1;1)\) и \(\vec{b}(0;7)\). Найдите длину вектора \(8\vec{a}+\vec{b}\)

Даны векторы \(\vec{a}(5;3)\) и \(\vec{b}(4;-6)\). Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)

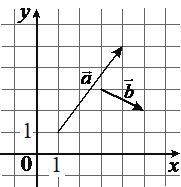
На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\), координатами которых являются целые числа. Найдите длину вектора \(\vec{a}+4\vec{b}\)

​

Даны векторы \(\vec{a}(31;0)\) и \(\vec{b}(1;-1)\). Найдите длину вектора \(\vec{a}-24\vec{b}\)

Даны векторы \(\vec{a}(14;-2)\) и \(\vec{b}(5;-8)\). Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)

Даны векторы \(\vec{a}(-3;5)\) и \(\vec{b}(1;13)\). Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)

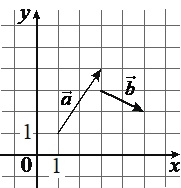
На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\), координатами которых являются целые числа. Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)

​

Даны векторы \(\vec{a}(2;0)\) и \(\vec{b}(1;4)\). Найдите длину вектора \(\vec{a}+3\vec{b}\)

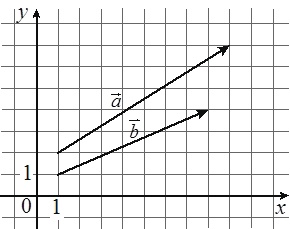
На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\), координатами которых являются целые числа. Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)

​

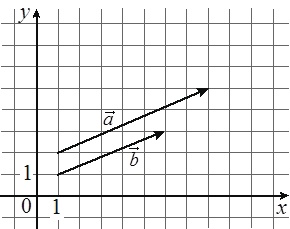
На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\), координатами которых являются целые числа. Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)

Даны векторы \(\vec{a}(5;-7)\) и \(\vec{b}(14;1)\). Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)

Длины векторов \(\vec{a}\) и \(\vec{b}\) равны 3 и 5, а угол между ними равен 60°. Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)

Длины векторов \(\vec{a}\) и \(\vec{b}\) равны 3 и 7, а угол между ними равен 60°. Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)