Варианты ЕГЭ база (с разбором)
Содержание
Вариант ЕГЭ база 2.19
Вычислите \(3{\dfrac{8}{15}}-0{,}2\cdot 2{\dfrac23}\).
Вычислите \(\dfrac{\left( 5^{-7}\right)^3}{5^{-19}}\).
Акции предприятия разделены между государством и частными лицами в отношении 1:5 соответственно. Общая прибыль предприятия после уплаты налогов за год составила 36 млн рублей. Какая сумма от этой прибыли должна пойти на выплату частным акционерам? Ответ дайте в миллионах рублей.
Мощность постоянного тока (в ваттах) вычисляется по формуле \(P=I^2 R\), где \(I\) – сила тока (в амперах), \(R\) – сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление \(R\) (в омах), если мощность составляет \(13{,}5\, Вт\), а сила тока равна \(1{,}5\, А\).
Вычислите \(\dfrac76\sqrt{10}\cdot \sqrt{90}\).
Принтер печатает одну страницу за 11 секунд. Какое наибольшее количество страниц можно напечатать на этом принтере за 8 минут?
Решите уравнение \(\log_7(2x-6)-\log_7{2}=\log_7{3}\).
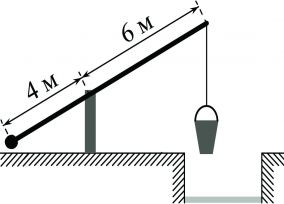
На рисунке изображен колодец с "журавлем". Короткое плечо имеет длину 4м, длинное плечо – 6м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1м?
Установите соответствие между величинами и их возможными значениями. Запишите в ответ цифры в порядке, соответствующем буквам АБВГ.
| ВЕЛИЧИНЫ | ЗНАЧЕНИЯ |
| А. масса блокнота | 1) 16 т |
| Б. масса новорожденного ребенка | 2) 3400 г |
| В. масса трамвая | 3) 80 г |
| Г. масса кухонного холодильника | 4) 41 кг |
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме "Подобие треугольников" равна 0,3. Вероятность того, что это вопрос по теме "Свойства биссектрисы" равна 0,11. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите веростность того, что на эказмене школьнику достанется вопрос по одной из этих двух тем.
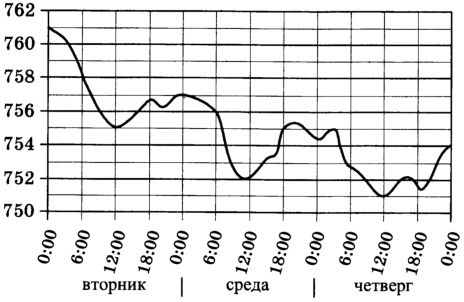
На рисунке изображен график изменения атмосферного давления в течение трех суток. По горизонтали указаны дни недели, по вертикали – значения давления в миллиметрах ртутного столба. Определите по рисунку значение атмосферного давления в 12:00 во вторник.
В таблице приведены данные о шести чемоданах.
| Номер чемодана | Длина (см) | Высота (см) | Ширина (см) | Масса |
| 1 | 64 | 38 | 27 | 25 |
| 2 | 78 | 45 | 13 | 22,5 |
| 3 | 67 | 67 | 45 | 21 |
| 4 | 58 | 45 | 25 | 36 |
| 5 | 64 | 56 | 50 | 24 |
| 6 | 58 | 49 | 39 | 21,5 |
По правилам авиакомпании сумма трёх измерений (длина, высота, ширина) чемодана, сдаваемого в багаж, не должна превышать 158 см, а масса не должна быть больше 23 кг. Какие чемоданы можно сдать в багаж по правилам этой авиакомпании? В ответе укажите номера выбранных чемоданов без пробелов, запятых и других дополнительных символов.
Вода в цилиндрическом сосуде находится на уровне h=50 см. На каком уровне будет находиться вода, если её перелить в другой цилиндрический сосуд, радиус основания которого в 2,5 раза больше, чем у первого? Ответ дайте в сантиметрах.
На рисунке изображены график функции и касательные к нему в точках с абсциссами A, B, C и D.
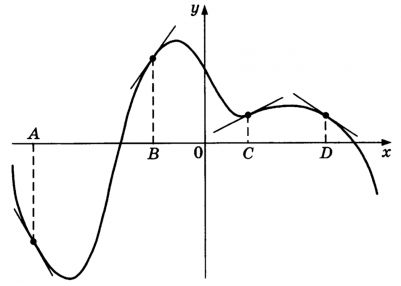
В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней. Ответ запишите в порядке, соответствующем точкам A, B, C, D.
| ТОЧКИ | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
| A | 1. 0,5 |
| B | 2. 1,4 |
| C | 3. -1,8 |
| D | 4. -0,7 |
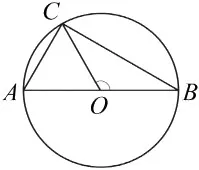
В окружности с центром \(O\) проведен диаметр \(AB\) и взята точка \(C\) так, что угол \(COB=120°\), \(AC=18\). Найдите диаметр этой окружности.
Два ребра прямоугольного параллелепипеда равны 12 и 5, а объем параллелепипеда равен 480. Найдите площадь поверхности этого параллелепипеда.
Число \(a\) равно \(\sqrt6\). Каждому из четыреxчисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца. В ответ запишите цифры в порядке, соответствующем буквам АБВГ.
| ЧИСЛА | ОТРЕЗКИ |
| А. \(-\sqrt{a}\) | 1. [-2;-1] |
| Б. \(a^2-4\) | 2. [-1;0] |
| В. \(-\dfrac{a}{10}\) | 3. [0;1] |
| Г. \(\dfrac1{a}\) | 4. [1;2] |
Кондитер испёк 50 кексов, из них 15 кексов он посыпал корицей, а 20 кексовпосыпал сахаром. Выберите утверждения, которые верны при указанных условиях.
1) Не может оказаться больше 20 кексов, посыпанных и сахаром, и корицей.
2) Найдётся 20 кексов, посыпанных и сахаром, и корицей.
3) Если кекс посыпан сахаром, то он посыпан и корицей.
4) Найдётся 10 кексов, которые не посыпаны сахаром и корицей.
В ответе запишите номера выбранных утверждений по возрастанию без пробелов, запятых и других дополнительных символов.
Найдите четырехзначное число, кратное 45, все цифры которого различны и четны. В ответ укажите наибольшее из таких чисел.
Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами – 352, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?