Разбор вариантов ОГЭ
Содержание
Вариант ОГЭ 12.18
Алгебра
\( \boxed{1} \) Найдите значение выражения: \( 5{,}2\cdot 3{,}2+0{,}13\).
\( \boxed{2} \) Гарвиил ежедневно в течение недели измерял время, которое он тратил, стоя в пробке по дороге на работу, а результаты записывал в таблицу.
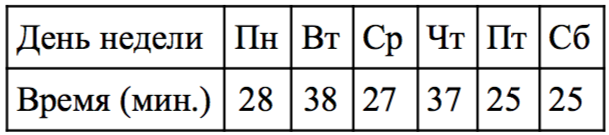
Сколько минут в день в среднем тратил Гавриил, стоя в пробке по дороге на работу?
\( \boxed{3} \) Числа \(a\) и \(b\) отмечены точками на на координатной прямой. Расположите в порядке убывания числа \( \dfrac1{a}\), \( \dfrac1{b}\) и 1.

1) \( \dfrac1{a}; \dfrac1{b}; 1\)
2) \( \dfrac1{b}; \dfrac1{a}; 1\)
3) \( \dfrac1{b}; 1 ; \dfrac1{a}\)
4) \( \dfrac1{a}; 1; \dfrac1{b}\)
\( \boxed{4} \) Найдите значение выржения \( \dfrac{6^{-7}\cdot 6^{-8}}{6^{-13}} \).
1) -36
2) \(-\dfrac1{36}\)
3) 36
4) \(\dfrac1{36}\)
\( \boxed{5} \) На графике показано, сколько человек приняли участие в конкурсе с 13 января по 4 марта. По горизонтали указаны числа месяцев, а по вертикали — количество человек.
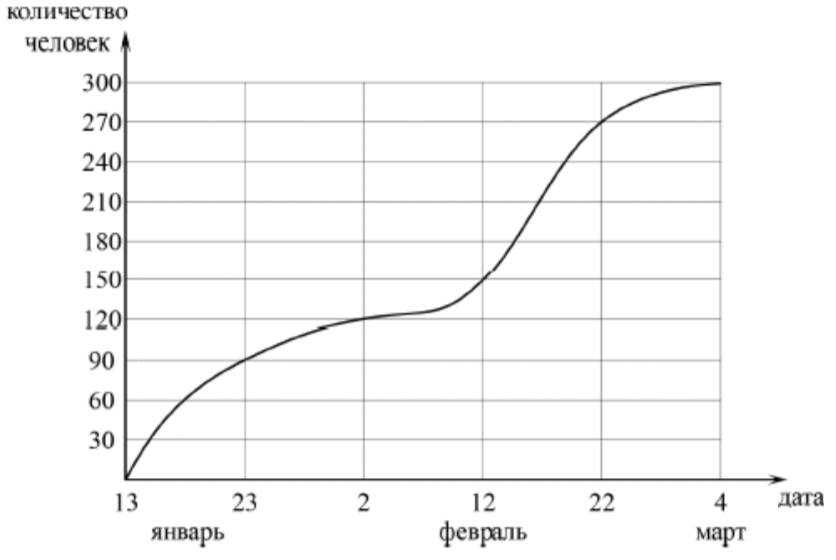
Во сколько раз возросло количество участников с 2 по 22 февраля?
\( \boxed{6} \) Решите уравнение \(x^2-11x+18=0\). Если корней несколько, в ответ запишите больший из них.
\( \boxed{7} \) В начале года число зарегистрированных пользователей сайта составляло 160 тысяч человек, а в конце года их стало 180 тысяч. На сколько процентов увеличилось число зарегистрировавшихся на этом сайте пользователей за год?
\( \boxed{8} \) На диаграмме представлены семь крупнейших по площади территории (в млн км\(^2\)) стран мира.
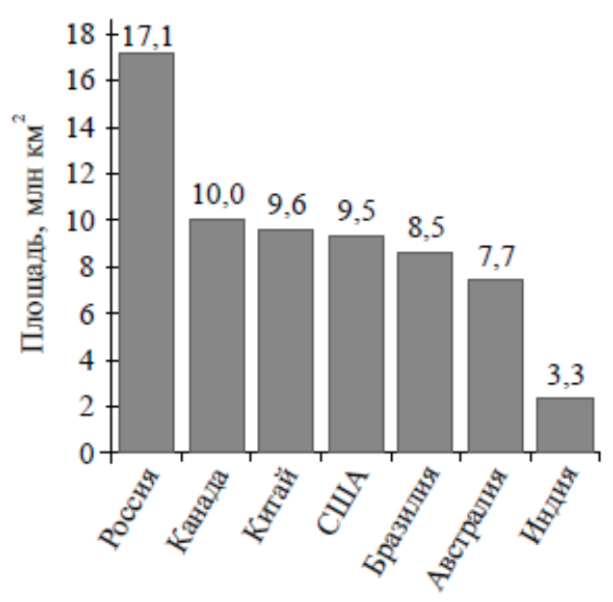
Запишите номера неверных утверждений (без пробелов, в порядке возрастания).
1) Суммарная площадь США и Канады меньше площади России.
2) Площадь России больше площади Австралии более, чем в 2 раза.
3) Площади США и Китая отличаются меньше, чем на 0,5 млн км\(^2\).
4) Бразилия – четвертая по площади страна мира.
\( \boxed{9} \) У Аристарха сломался телевизор и показывает только один случайный канал. Аристарх включает телевизор. В это время по 7 каналам из 20 показывают детективы. Найдите веростность того, что Аристарх попадет на канал, где не показывают детектив.
\( \boxed{10} \) График какой функции изображен на рисунке?
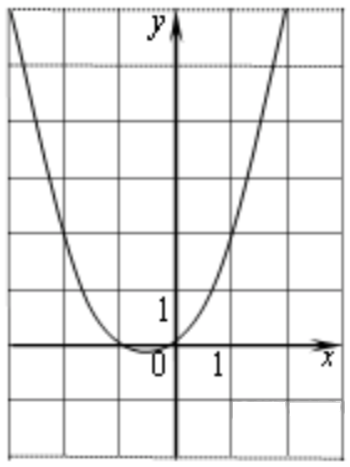
1) \( y=-x^2-x\)
2) \( y=x^2-x\)
3) \( y=-x^2+x\)
4) \( y=x^2+x\)
\( \boxed{11} \) Выписаны первые несколько членов геометрической прогрессии: 13, 52, 208. Найдите её пятый член.
\( \boxed{12} \) Найдите значение выражения \( \dfrac{a^2+18x+81}{a}:\left( \dfrac9{a}+1\right) \) при \( a=-\dfrac{13}{2}\)
\( \boxed{13} \) За 20 минут велосипедист проехал 7 километров. Сколько километров он проедет за 37 минут, если будет ехать с той же скоростью?
\( \boxed{14} \) Решите неравенство \(x^2+2x\geqslant 0 \). В ответ укажите номер правильного варианта.
1) \( (-\infty; -2]\cup [0;+\infty) \)
2) \( [-2;0]\)
3) \( [0;2]\)
4) \( (-\infty; 0]\cup [2;+\infty) \)
Геометрия
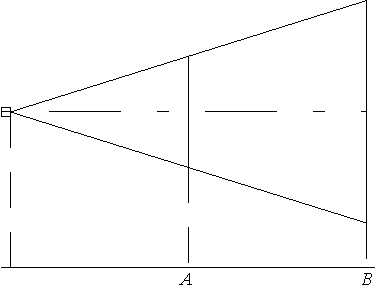
\( \boxed{15} \) Проектор полностью освещает экран A высотой 60 см, расположенный на расстоянии 150 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 180 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
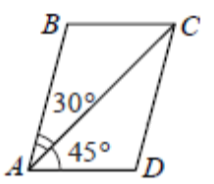
\( \boxed{16} \) Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
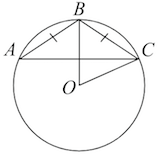
\( \boxed{17} \) Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 138°. Найдите величину угла BOC. Ответ дайте в градусах.
\( \boxed{18} \) Сторона прямоугольника равна 8, диагональ равна 10. Найдите площадь этого прямоугольника.
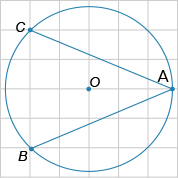
\( \boxed{19} \) Найдите \( \mathrm{tg\,} BAC \).
\( \boxed{20} \) Какие из данных утверждений верны?
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат.
4) Если две прямые перпендикулярны третьей, то эти две прямые перпендикулярны.
Запишите номера верных утверждений в порядке возрастания.