Разбор вариантов ОГЭ
Содержание
ОГЭ 4.19
Вычислите \(28\cdot\left( \dfrac14\right)^2-14\cdot \dfrac14\)
Куриные яйца в зависимости от их массы подразделяют на пять категорий: высшая, отборная, первая, вторая и третья. Используя данные, представленные в таблице, определите, к какой категории относится яйцо, массой 61,3г. (В ответ впишите номер категории)
| Категория | Масса одного яйца, не менее, г. |
| 1. Высшая | 75 |
| 2. Отборная | 65 |
| 3. Первая | 55 |
| 4. Вторая | 45 |
| 5. Третья | 35 |
Какое из данных чисел принадлежит промежутку [7;8]?
1) \(\sqrt{7}\)
2)\(\sqrt{8}\)
3)\(\sqrt{48}\)
4)\(\sqrt{59}\)
Какое из данных выражений при любых значениях \(n\) равно дроби \(\dfrac{4^n}{16}\)?
1) \(2^{2n-2}\)
2) \(4^{\frac{n}{2}}\)
3) \(2^{2n-4}\)
4) \(\left(\dfrac14\right)^n\)
На графике изображена зависимость атмосферного давления от высоты над уровнем моря. По горизонтали указана высота над уровннем моря в километрах, по вертикали — атмосферное давление в мм ртутного столба. На сколько мм ртутного столба давление на высоте 3,5 км выше, чем на высоте 6,5 км?
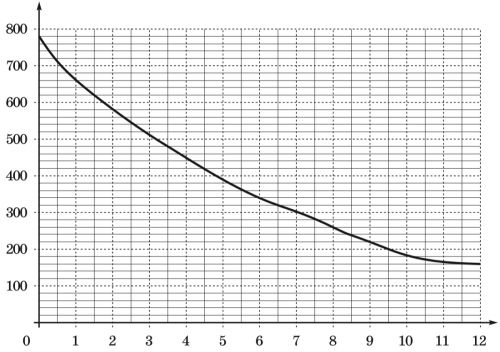
Произведение двух последовательных натуральных чисел на 239 больше их суммы. Найдите меньшее из этих чисел.
После повышения цены на 30% товар стал стоить 1040 рублей. Сколько стоил этот товар до подорожания?
Какая из круговых диаграмм показывает распределение площадей океанов в мировом Океане, если Тихий Океан занимает около 49% всего Мирового Океана, атлантический — 26%, Индийский — 21% и Северный Ледовитый — 4%?
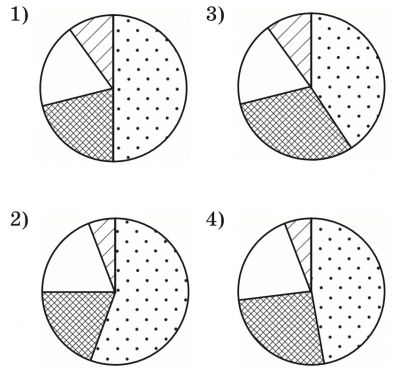
В магазине продается 200 ручек. Из них 46 черные, 85 синие, 44 красные и остальные зеленые. Найдите вероятность того, что случайно выбранная ручка будет синей или зеленой.
Установите соответствие между функциями и их графиками.
А) \(y=-\dfrac2{x}\)
Б) \(y=-\dfrac1{2x}\)
В) \(y=\dfrac2{x}\)
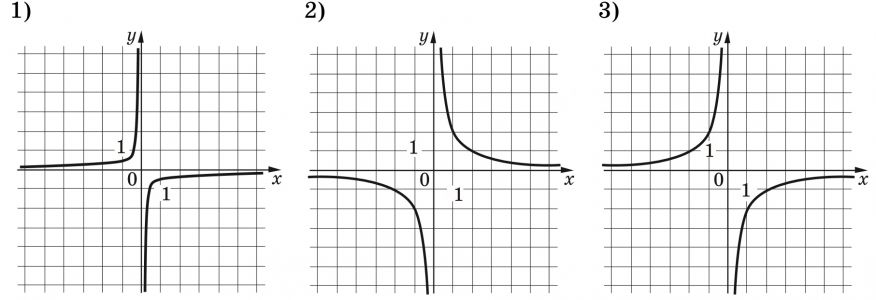
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: АБВ.
Выписаны несколько последовательных членов геометрической прогрессии: \(...; -15; x; -0{,}6; 0{,}12;...\). Найдите \(x\).
Найдите значение выражения \(\dfrac{a^2-49b^2}{7ab}:\left( \dfrac{1}{7b}-\dfrac1{a}\right)\) при \(a=4{\frac{5}{19}}\), \(b=6{\frac{2}{19}}\).
Значение температуры по шкале Цельсия переводится в значение температуры по шкале Фаренгейта по формуле \(t_{F}=1{,}8 t_C+32\), где \(t_C\) — температура в градусах Цельсия, \(t_F\) — температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует -40° по шкале Цельсия?
Решите неравенство \(\dfrac{5x-7}{22-2x}\geqslant 0\). В ответ запишите наибольшее целое число, являющееся решением данного неравенства.
Руслан прошел от дома по направлению на восток 650 м, затем повернул на юг и прошел еще 720 м. На каком расстоянии от дома (в метрах) он оказался?
В прямоугольном треугольнике ABC с прямым углом C катет AC=8, \(\cos A=\dfrac47\). Найдите AB.
В угол A, величиной 18°, вписана окружность, которая касается сторон угла в точках B и C, точка O — центр окружности. Найдите угол BOC, ответ дайте в градусах.
Найдите периметр прямоугольника, если его длина равна 8, а диагональ 10.
На клетчатой бумаге с размером клетки \(\sqrt2\times \sqrt2\) изображен треугольник ABC. Найдите длину его медианы, проведенной из вершины A.
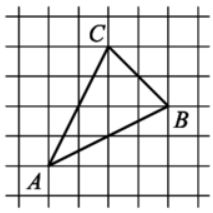
Укажите номера верных утверждений.
1) Диагональ прямоугольника равна диаметру описанной около него окружности.
2) Если три угла одного треугольника равны трем углам другого треугольника,то то такие треугольники равны.
3) Расстояние между двумя точками, лежащими на одной окружности, не превосходит удвоенного радиуса.
Запишите номера верных утверждений по возрастанию, без пробелов и дополнительных символов.
Решите систему уравнений \(\begin{cases}3x^2+2y=9\\ 7x^2-2y=1\end{cases}\)
Поезд, двигаясь равномерно со скоростью \(36 \,км/ч\), проезжает мимо фонарного столба за 54 секунды. Найдите длину поезда в метрах.
Постройте график функции \(y=\dfrac{4|x|-1}{|x|-4x^2}\) и определите, при каких значениях \(k\) прямая \(y=kx\) не имеет с графиком ни одной общей точки.
Запишите значения \(k\) по возрастанию, через точку с запятой, без пробелов.
В прямоугольном треугольнике ABC с прямым углом B проведена высота BH. Найдите AH, если AB=16, AC=20.
В параллелограмме ABCD точка K — середина стороны CD. Известно, что AK=BK. Докажите, что данный параллелограмм — прямоугольник.
В выпуклом четырехугольнике ABCD диагональ AC является биссектрисой угла BAD и пересекается с диагональю BD в точке O. Найдите AO, если известно, что около четырехугольника ABCD можно описать окружность, BC=20, OC=16.