Разбор вариантов ОГЭ
Содержание
ОГЭ 7.19
Найдите значение выражения \(\left( \dfrac13+8{,}6\right)\cdot \dfrac34\).
В таблице приведен норматив по прыжкам в длину с разбега для учащихся 9 классов.
| Мальчики | Девочки | |||||
| Отметка | "5" | "4" | "3" | "5" | "4" | "3" |
| Длина (метры) | 4,2 | 4,0 | 3,6 | 3,5 | 3,1 | 2,7 |
Какую отметку получит девочка, прыгнувшая на 3 метра 17 сантиметров?
1) Отметка "5"
2) Отметка "4"
3) Отметка "3"
4) Норматив не выполнен
Какое из следующихнеравенств не следует из неравенства \(3x-4y<5z\)?
1) \(3x-4y-5z<0\)
2) \(4y+5z>3x\)
3) \(0{,}6x+z<0{,}8y\)
4) \(0{,}75x<1{,}25z+y\)
Найдите значение выражения \((3{,}2\cdot 10^{-1})\cdot (3\cdot 10^3)\).
Температура жидкости в резервуаре в результате нагревания со временем постепенно увеличивается. На оси абсцисс откладывается время в минутах, прошедшее с момента начала нагревания, на оси ординат — температура жидкости в резервуаре в градусах Цельсия.
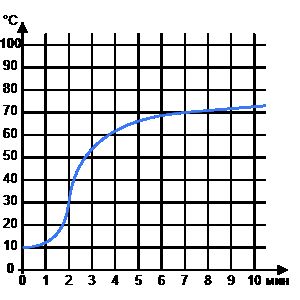
Определите по графику, за сколько минут жидкость нагреется с 30 до 70 градусов.
Решите уравнение \((2x-1)^2=3x^2-4x+17\). Если уравнение имеет более одного корня, в ответ укажите меньший из корней.
На витрине ювелирного магазина представлено 40 изделий. 36 из них золотые, остальные из серебра. В каком отношении на витрине представлены золотые и серебряные изделия?
1) 13:1
2) 9:1
3) 2:3
4) 3:7
На диаграмме представлена информация о количестве жителей шести самых населённых городов некоторой страны.
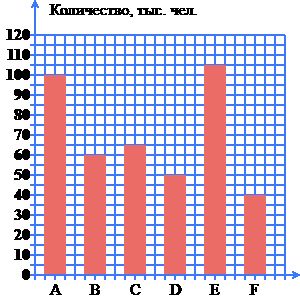
Какие из следующих утверждений являются неверными? Запишите номера неверных утверждений в порядке возрастания без дополнительных символов.
1) Город C входит в тройку наименее населённых городов среди представленных на диаграмме.
2) Город F является самым населённым.
3) Город E является самым населённым.
4) Город D входит в тройку наименее населённых городов среди представленных на диаграмме.
На научной конференции будут выступать 27 докладчиков, среди которых 5 докладчиков из Японии, 6 из России. Шестым выступает докладчик из России, а перед ним выступает докладчик из Японии. Найдите вероятность того, что седьмым тоже выступает докладчик из Японии, если порядок выступлений определяется жребием.
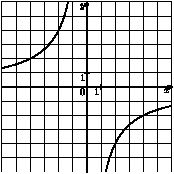
На рисунке изображена гипербола — график функции \(y=\dfrac{k}{x}\). Найдите значение коэффициента \(k\).
Арифметическая прогресия задана формулой \(a_n=1-4n\). Чему равна разность \(d\) этой прогрессии?
Упростите выражение \({\left(\sqrt{189}-a\right)^2-\left(\sqrt{189}-a\right)\left(a+\sqrt{189}\right)+2 \cdot a \cdot \sqrt{189}}\) и найдите его значение при \(a=\sqrt{89}\).
Формула кинетической энергии тела \(E=\dfrac{mv^2}{2}\). Найдите скорость тела с кинетической энергией \(80\,\dfrac{кг\cdot м^2}{с^2}\), если масса этого тела равна 10 кг. Ответ дайте в км/ч.
Укажите номер рисунка, на котором изображено множество решений неравенства \(-5x-10\left(-2x+5\right)-9\geqslant 8x-3\).
1)
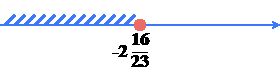
2)
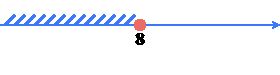
3)
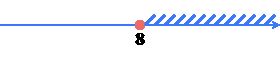
4)
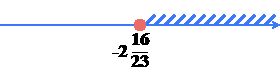
Два велосипедиста одновременно выехали из одного пункта, один на север, другой на восток. Какое расстояние в (км) будет между ними через 3 часа, если их скорости 15 км/ч и 20 км/ч?
Найдите острый угол между высотами равностороннего треугольника. Ответ дайте в градусах.
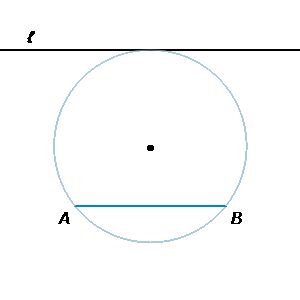
A и B — точки окружности. Длина хорды AB равна \(2\sqrt{561}\). Расстояние от хорды AB до параллельной ей касательной \(l\) равно 33. Найдите радиус этой окружности.
Основания равнобедренной трапеции равны 4 и 2. Боковая сторона равна \(\sqrt{82}\). Найдите площадь трапеции.
Найдите косинус угла, изображенного на рисунке.

Укажите номера неверных утверждений.
1) Сумма углов шестиугольника равна 360°.
2) Диагонали прямоугольника перпендикулярны.
3) Диагонали ромба точкой пересечения делятся пополам.
4) Периметр прямоугольника равен удвоенному произведению длин его смежных сторон.
Номера запишите в порядке возрастания, без пробелов и запятых.
Найдите значение выражения \(\dfrac{\sqrt{(\sqrt{131}-\sqrt{31})(\sqrt{131}+\sqrt{31})}}2\)
Двое рабочих могут выполнить всю работу за 1 час 12 минут. За сколько минут выполнит всю работу первый рабочий, если известно, что он работает в полтора раза медленнее второго?
Постройте график функции \(y=\begin{cases}-\dfrac1{x}\;при\, x<-1\\ |x^2|-2\;при \, x\geqslant -1\end{cases}\)
и определите, при каких значениях \(m\) прямая \(y=m\) имеет с графиком ровно одну общую точку.
Найдите радиус окружности, описанной около треугольника со сторонами 5, 6, 9.
Докажите, что если окружность касается сторон AB и AC треугольника ABC в точках B и C, и биссектриса AD угла BAC пересекает меньшую из двух дуг BC в точке N, то CN — биссектриса угла ACB.
Дан треугольник \(ABC\), высоты \(AA_1\), \(BB_1\) и \(CC_1\) которого относятся как 6:4:3. Найдите длину меньшей стороны треугольника \(ABC\), если его периметр равен 99.