Разбор вариантов ОГЭ
Содержание
ОГЭ 1.19
Найдите значение \(n\), при котором верно равенство \(0{,}3\cdot 0{,}003\cdot 0{,}00003=27\cdot 10^{n}\)
В таблице приведены нормативы по отжиманиям для учащихся 9 класса. Какую оценку получит мальчик, отжавшийся 30 раз?
| Мальчики | Девочки | |||||
| Количество раз | 32 | 27 | 22 | 20 | 15 | 10 |
| Оценка | 5 | 4 | 3 | 5 | 4 | 3 |
На координатной прямой отмечены числа \(a\), \(b\) и \(c\).
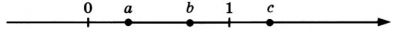
Укажите номера верных утверждений:
1) \(a^2>c\)
2) \(\dfrac1{a}>\dfrac1{c}\)
3) \(b^2>1\)
4) \(-\dfrac1{b}<\dfrac1{c}\)
Найдите значение выражения \((\sqrt7+2)(\sqrt7-2)\).
На графике показано, как изменяется атмосферное давление в зависимости от изменения высоты над уровнем моря. На оси абсцисс отмечена высота над уровнем моря в метрах, на оси ординат – атмосферное давление в мм ртутного столба. Высота горы Элберт равна приблизительно 4500 м. На сколько (в мм рт. ст.) атмосферное давление на ее вершине выше давления на высоте 9000 м?
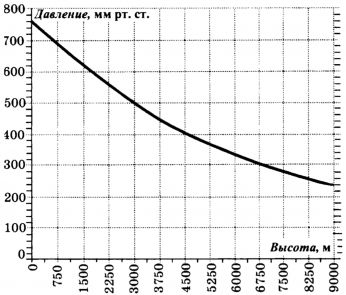
Решите уравнение \(\dfrac{x-3}{x-5}=\dfrac34\).
Номер в гостинице стоил 1800 рублей в сутки. Но перед Новым годом стоимость проживания поднялась на 20%, а после праздников понизилась на 20%. Сколько рублей стал стоить этот номер в сутки после понижения цены?
На диаграмме показано содержание питательных веществ в сливочных сухарях. Определите по диаграмме, в каких пределах находится содержание углеводов.
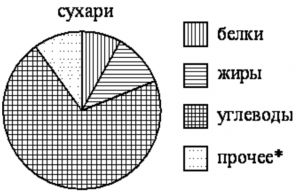
*к прочему относятся вода, витамины и мине ральные вещества.
1) 45-55%
2) 55-65%
3) 65-75%
4) 75-80%
На конференцию приехали 9 ученых из России, 7 из Белоруссии, 6 из Узбекистана и 3 из Армении. Порядок чтения докладов определяется жеребьевкой. Найдите вероятность того, что пятым будет выступать ученый из Армении.
График какой из перечисленных ниже функций представлен на рисунке?
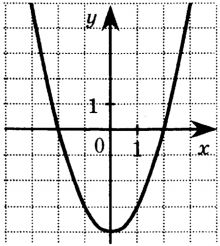
1) \(y=(x-4)^2\)
2) \(y=x^2-4\)
3) \(y=(x-2)^2\)
4) \(y=x^2-2\)
Геометрическая прогрессия \(b_n\) задана условиями \(b_1=-\dfrac1{27}\), \(b_{n+1}=3b_n\). Найдите пятый член этой прогрессии.
Сократите дробь \(\dfrac{(a+b)^2-(a-b)^2}{5ab}\).
Площадь трапеции можно вычислить по формуле \(S=\dfrac{a+b}{2}\cdot h\), где \(a\) и \(b\) – основания, \(h\) – высота трапеции. Найдите \(a\), если \(S=128, \; h=16,\; b=6\).
Выберите верное множество решений неравенства \(x^2-2x-3\geqslant 0\).
1) (-∞;-1)∪(3;+∞)
2) (-1;3)
3) (-∞;-1]∪[3;+∞)
4) [-1;3]
Какой угол (в градусах) образуют минутная и часовая стрелки в 19:00?
Медиана равностороннего треугольника равна \(7\sqrt3\). Найдите его сторону.
Радиус \(OB\) окружности с центром в точке \(O\) пересекает хорду \(AC\) в точке \(D\) и перпендикулярен ей. Найдите длину хорды \(AC\), если \(BD = 2 \,см\), а радиус окружности равен \(10 \,см\).
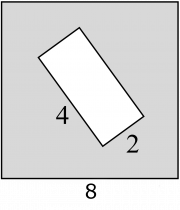
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
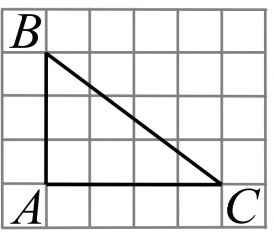
Найдите тангенс угла C треугольника ABC, изображенного на рисунке.
Укажите номера верных утверждений.
1) Через любую точку проходит не менее одной прямой.
2) Если при пересечении двух прямых третьей прямой соответственные углы равны 25°, то эти две прямые параллельны.
3) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.
Если утверждений несколько, запишите их номера в порядке возрастания без запятых и пробелов.
Решите уравнение \((x+3)^4-4(x+3)^2-21=0\)
Из города А в город В выехал автобус. Через 30 минут вслед за ним выехал автомобиль. Через 2ч 12мин после своего выезда, обогнав автобус, автомобиль отдалился от него на 14 км. Найдите скорость автобуса, если известно, что она на 20 км/ч меньше скорости автомобиля.
Постройте график функции \(y=|x^2-2x-3|\) и определите, при каких значениях \(n\) прямая \(y=n\) имеет с этим графиком ровно три общие точки.
Окружность пересекает стороны АВ и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK = 6, а сторона AC в 1,5 раза больше стороны BC.
Докажите, что медиана треугольника делит его на два треугольника, площади которых равны.
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 12, а площадь равна 18.
Запишите в ответ градусные меры этих углов по возрастанию через точку с запятой без пробелов.