Разбор вариантов ОГЭ
Содержание
ОГЭ 3.19
Вычислите \(\left( 0{,}8+\dfrac7{25}\right):\dfrac57\).
В таблице приведены нормативы по бегу на 60м для учащихся 9 класса.
| мальчики оценка "5" | мальчики оценка "4" | мальчики оценка "3" | девочки оценка "5" | девочки оценка "4" | девочки оценка "3" | |
| Время, секунды | 8,5 | 9,2 | 10,0 | 9,4 | 10,0 | 10,5 |
Какую оценку получит мальчик, пробежавший за 9,6 секунд?
1) "5"
2) "4"
3) "3"
4) норматив не выполнен
На координатной прямой отмечены точки A, B, C и D, соответствующие числам \(-0{,}82\); \(-0{,}072\); \(0{,}08\); \(-0{,}702\).
Какой точке соответствет число \(-0{,}072\)?
1) A
2) B
3) C
4) D
Найдите значение выражения \(\sqrt{0{,}0064}-\sqrt{0{,}64}\).
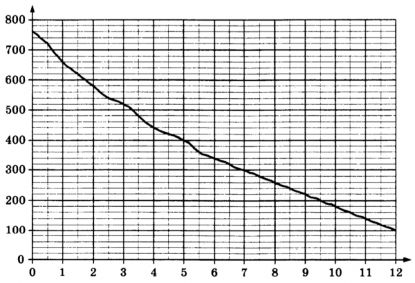
На графике изображена зависимость атмосферного давления от высоты над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в км, на вертикальной - давление в мм ртутного столба. Определите по графику, на какой высоте атмосферное давление равно 140 мм ртутного столба. Ответ дайте в км.
Решите уравнение \(x^2-77=4x\). Если корней несколько, в ответ запишите меньший из них.
Поступивший в сентябре в продажу ноутбук стоил 78000 рублей. В ноябре он стал стоить 81120 рублей. На сколько процентов за этот период повысилась его цена?
На диаграмме представлены семь крупнейших по площади территории (в млн \(км^2\)) стран мира.
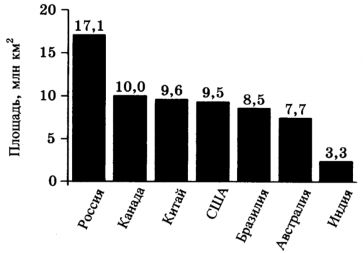
Какие из следующих утверждений не верны?
1) Площадь Канады больше площади Китая.
2) Площадь Австралии более, чем в 2 раза превышает площадь Индии.
3) Суммарная площадь США и Канады меньше площади России.
4) Суммарная площадь двух крупнейших стран мира больше суммарной плозщади всех остальных стран.
В каждой двадцать пятой упаковке чая под крышкой призовой код. Коды распределены по упаковкам случйно. Алишер покупает упаковку чая. Найдите вероятность того, в его упаковке не будет призового кода.
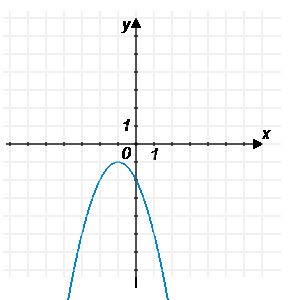
По графику функции \(y=ax^2+bx+c\), приведенному на рисунке, найдите коэффициент \(c\).
Арифметическая прогрессия задана условиями \(a_1=-9,\; a_{n+1}=a_n+4\). Найдите сумму первых шести её членов.
Найдите значение выражения \((2+x)^2-x(x-4)\) при \(x=\dfrac78\).
Площадь четырехугольника можно вычислить по формуле \(S=\dfrac{d_1\cdot d_2\cdot \sin\alpha}{2}\), где \(d_1\) и \(d_2\) —длины диагоналей четырехугольника, \(\alpha\) — угол между ними. Найдите длину диагонали \(d_1\), если \(d_2=14\), \(\sin \alpha=\dfrac37\), а \(S=18\).
Найдите наибольшее целое решение неравенства \(7x+15\geqslant 3-5(2-3x)\).
Две сосны растут на расстоянии 20м одна от другой. Высота одной сосны 21м, а другой 6м. Найдите расстояние (в метрах) между их верхушками.
В треугольнике ABC угол A равен 30°, угол B равен 45°, \(BC=8\sqrt2\). Найдите AC.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 168°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Сумма двух углов равнобедренной трапеции равна 148°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
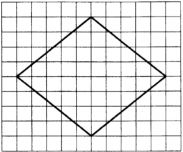
На клетчатой бумаге с размером клетки 1×1 изображен ромб. Найждите его площадь.
Какие из следующих утверждений верны?
1) Внутренние накрест лежащие углы при пересечении двух прямых секущей равны.
2) Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
3) Внешний угол треугольника равен сумме его внутренних углов.
4) Диагонали ромба перпендикулярны.
Решите уравнение \((x-8)^4-3(x-8)^2-10=0\)
Первая труба пропускает на 15 литров воды в минуту меньше, чем вторая труба. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 100 литров она заполняет на 6 минут дольше, чем вторая труба?
Постройте график функции \(y=-5-\dfrac{x-2}{x^2-2x}\). Определите, при каких значениях \(m\) прямая \(y=m\) не имеет с графиком общих точек.
Запишите значения m в десятичном виде по возрастанию, через точку с запятой, без пробелов.
Высота AH ромба делит его сторону CD на отрезки DH=12 и CH=1. Найдите высоту ромба.
Окружности с центрами в точках A и B пересекаются в точках C и D, причём точки A и B лежат по одну сторону от прямой CD. Докажите, что CD ⊥ AB.
Углы при одном из оснований трапеции равны 70° и 20°. А отрезки, соединяющие середины противоположных сторон, равны 20 и 17. Найдите основания трапеции.
В ответ запишите основания по возрастанию, через точку с запятой, без пробелов.