ОГЭ 2.20

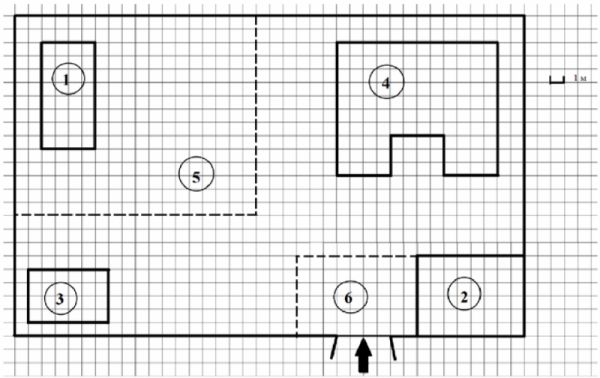
На плане изображено домохозяйство (сторона каждой клетки на плане равна 1 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота. При входе на участок слева от ворот находится сарай, а справа — гараж. Площадь, занятая гаражом, равна 48 кв. м. Жилой дом находится в глубине территории. Помимо гаража, жилого дома и сарая, на участке имеется теплица, расположенная на территории огорода (огород отмечен на плане цифрой 5). Перед гаражом имеется площадка, вымощенная тротуарной плиткой размером 0,2м ×0,1м и отмеченная на плане цифрой 6.

Решите уравнение \((2x-6)^2\cdot(x-6)=(2x-6)\cdot(x-6)^2\)

Найдите значение выражения \(-0{,}2\cdot (-10)^2+55\)

На координатной прямой точки A, B, C и D соответствуют числам 0,29; -0,02; 0,109 и 0,013.

Какой точке соответствует число 0,109?

1) A
2) B
3) C
4) D

Найдите значение выражения \((\sqrt{37}-5)(\sqrt{37}+5)\).

Решите уравнение \((-x-4)(3x+3)=0\). Если уравнение имеет более одного корня, то в ответ запишите больший из корней.

У бабушки 25 чашек: 7 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.

Установите соответствие между графиками функций и формулами, которые их задают.

ГРАФИКИ

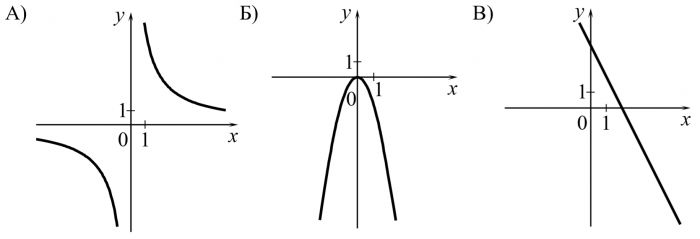
ФОРМУЛЫ

1) \(y=\dfrac6{x}\)

2) \(y=-2x+4\)

3) \(y=-2x^2\)

Последовательность (\(a_n)\) задана условями: \(a_1=5\), \(a_{n+1}=a_n+3\). Найдите \(a_8\).

Найдите значение выражения \(\dfrac{xy+y^2}{15x}\cdot \dfrac{3x}{x+y}\) при \(x=-9{,}5\) и \(y=-6\).

Площадь четырёхугольника можно вычислить по формуле \(S=\dfrac{d_1\cdot d_2\cdot \sin\alpha}{2}\), где \(d_1\) и \(d_2\) – длины диагоналей четырехугольника, \(\alpha\) – угол между диагоналями.Пользуясь этой формулой, найдите длину диагонали \(d_2\), если \(d_1=6\), \(\sin\alpha=\dfrac37\), \(S=18\).

Укажите решение системы неравенств

\(\begin{cases} -12+3x<0\\9-4x>-23\end{cases}\)

1) \((-\infty; 8)\)
2) \((-\infty; 4)\)
3) \((4; 8)\)
4) \((4; +\infty)\)

В треугольнике ABC известно, что ∠BAC=46°, AD – биссектриса. Найдите угол∠BAD. Ответ дайте в градусах.

На окружности взяты точки A и B так, что меньшая дуга AB равна 56°. Прямая BC касается окружности в точке B так, что∠ABCострый. Найдите угол∠ABC, ответ дайте в градусах.

Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 17 и 19. Найдите длину основания BC.

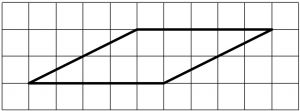
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Какие из следующих утверждений верны?
1)Средняя линия трапеции равна сумме её оснований.
2)Диагонали ромба перпендикулярны.
3)Площадь треугольника меньше произведения двух его сторон.

В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Решите неравенство \((x-5)^2<\sqrt7(x-5)\).

Баржа прошла по течению реки 80 км и, повернув обратно, прошла ещё 60 км, затратив на весь путь 10 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч. Ответ дайте в км/ч.

Постройте график функции

\(y=\dfrac{3|x|-1}{|x|-3x^2}\)

Определите, при каких значениях \(k\) прямая \(y= kx\) не имеет с графиком общих точек.

Запишите найденные значения \(k\) по возрастанию через точку с запятой без пробелов.

Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK=6 , а сторона AC в 1,5 раза больше стороны BC.

Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.

Углы при одном из оснований трапеции равны 80° и 10°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 20 и 17. Найдите основания трапеции.

Запишите их в ответ по возрастанию через точку с запятой без пробелов.