Ежедневные тесты
Меню курса
Ноябрь
Беседа ВК для обсуждения тестов: Вступить
Сложность теста - это диапазон сложности задач, которые в этот тест попали. Сложность задачи на сайте - это процент неверных ответов на неё.
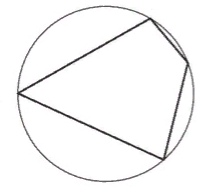
Два угла вписанного в окружность четырехугольника равны 99° и 117°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
Даны векторы \(\vec{a}(31;0)\) и \(\vec{b}(1;-1)\). Найдите длину вектора \(\vec{a}-24\vec{b}\)
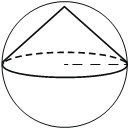
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 60. Найдите объём конуса.
Фабрика выпускает сумки. В среднем 4 сумки из 50 имеют скрытый дефект. Найдите вероятность того, что купленная сумка окажется без скрытого дефекта.
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в первом автомате закончится кофе, равна 0,1. Вероятность того, что кофе закончится во втором автомате, такая же. Вероятность того, что кофе закончится в обоих автоматах, равна 0,03. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Найдите корень уравнения \(2^{x-3}=\dfrac1{16}\)
Найдите значение выражения \(3\cos2\alpha\), если \(\sin\alpha=0{,}2\)
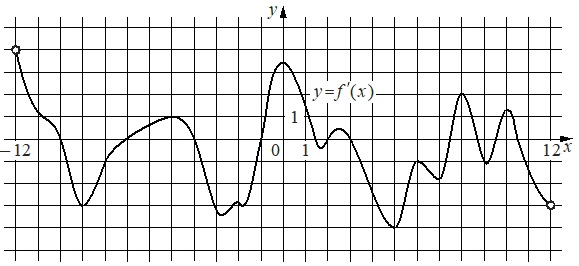
На рисунке изображен график y=f'(x) – производной функции f(x), определенной на интервале (-12;12). Найдите количество точек максимума функции f(x), принадлежащих отрезку [-6;11].
Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в К) от времени работы: \(T(t)=T_0+bt+at^2\), где \(t\) - время (в мин.), \( T_0=1600\) K, \(a=-5\) К/мин², \(b=105\) К/мин. Известно, что при температуре нагревательного элемента свыше 1870 К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.
По двум параллельным железнодорожным путям навстречу друг другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 85 км/ч и 35 км/ч. Длина пассажирского поезда равна 250 метрам. Найдите длину скорого поезда, если время, за которое он прошёл мимо пассажирского, равно 30 секундам. Ответ дайте в метрах.
На рисунке изображен график функции \(f(x)=ax^2+bx+c\). Найдите \(f(-3)\)
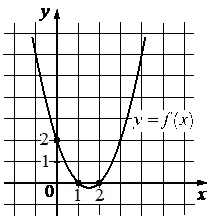
Найдите наибольшее значение функции \(y=\ln(x+9)^5-5x\) на отрезке [-8,5;0]
а) Решите уравнение \( \cos2x+\sin\left(\dfrac{\pi}2+x\right)+1=0\)
б) Найдите все корни этого уравнения, принадлежащие промежутку \(\left[-\dfrac{5\pi}{2}; -\pi\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4.π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -5π/2 | 18. -7π/3 | 19. -9π/4 | 20. -13π/6 |
| 21. -2π | 22. -11π/6 | 23. -7π/4 | 24. -5π/3 |
| 25. -3π/2 | 26. -4π/3 | 27. -5π/4 | 28. -7π/6 |
| 29. -π |
Решите неравенство \(\log_{0{,}3}(12-6x)\leqslant \log_{0{,}3}(x^2-6x+8)+\log_{0{,}3}(x+3)\)
В июле 2026 года планируется взять кредит в банке на пять лет в размере S тысяч рублей. Условия его возврата таковы:
— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле 2027, 2028 и 2029 долг остаётся равным S тысяч рублей;
— выплаты в 2030 и 2031 годах равны по 360 тысяч рублей;
— к июлю 2031 долг будет выплачен полностью.
Найдите общую сумму выплат за пять лет. Ответ дайте в тысячах рублей.