Ежедневные тесты
Меню курса
Октябрь
Беседа ВК для обсуждения тестов: Вступить
Сложность теста - это диапазон сложности задач, которые в этот тест попали. Сложность задачи на сайте - это процент неверных ответов на неё. 95+% задач сайта взяты из ФИПИ, сборников Ященко или полностью аналогичны им.
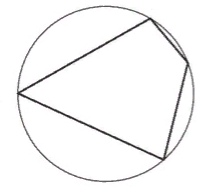
Два угла вписанного в окружность четырехугольника равны 59° и 102°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
Даны векторы \(\vec{a}(25;0)\) и \(\vec{b}(1;-5)\). Найдите длину вектора \(\vec{a}-4\vec{b}\)
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объём этой призмы, если объем отсечённой треугольной призмы равен 15.

На конференцию приехали учёные из трёх стран: 7 из Сербии, 3 из России и 2 из Дании. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что десятым окажется доклад учёного из России.
Помещение освещается тремя лампами. Вероятность перегорания каждой лампы в течение года равна 0,7. Лампы перегорают независимо друг от друга. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Найдите корень уравнения \(\log_4(x-4)=3\)
Найдите значение выражения \(3\sqrt2\cos^2\dfrac{9\pi}8-3\sqrt2\sin^2\dfrac{9\pi}8\)
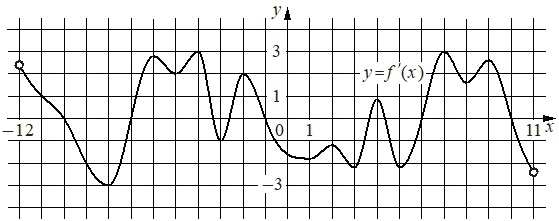
На рисунке изображен график y=f'(x) – производной функции f(x), определенной на интервале (-12;11). Найдите количество точек максимума функции f(x), принадлежащих отрезку [-11;5].
Мотоциклист, движущийся по городу со скоростью \(v_0=70\)км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением \(a=16\)км/ч². Расстояние (в км) от мотоциклиста до города вычисляется по формуле \(S=v_0 t+\dfrac{a t^2}{2}\), где \(t\) - время в часах, прошедшее после выезда из города. Определите время, прошедшее после выезда мотоциклиста из города, если известно, что за это время он удалился от города на 123 км. Ответ дайте в минутах.
Теплоход проходит по течению реки до пункта назначения 609 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 25 км/ч, стоянка длится 1 час, а в пункт отправления теплоход возвращается через 51 час после отплытия из него. Ответ дайте в км/ч.
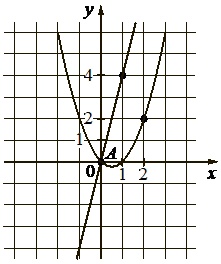
На рисунке изображены графики функций \(f(x)=ax^2+bx+c\) и \(g(x)=kx\), пересекающиеся в точках А и В. Найдите абcциссу точки В.
Найдите наименьшее значение функции \(y=12\cos x+\dfrac{45x}{\pi}-4\) на отрезке \(\left[-\dfrac{2\pi}3;0\right]\)
а) Решите уравнение \( \cos2x+\sin\left(\dfrac{\pi}2-x\right)+1=0\)
б) Укажите корни этого уравнения, принадлежащие отрезку \(\left[\dfrac{3\pi}2; 3\pi\right]\)
Запишите номера всех верных ответов на пункты а) и б) по возрастанию, через запятую, без пробелов. В первое поле на пункт а), во второе - на пункт б)
a)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 3π/2 | 18. 5π/3 | 19. 7π/4 | 20. 11π/6 |
| 21. 2π | 22. 13π/6 | 23. 9π/4 | 24. 7π/3 |
| 25. 5π/2 | 26. 8π/3 | 27. 11π/4 | 28. 17π/6 |
| 29. 3π |
Решите неравенство \(\log_{5}{\left((3-x)(x^2+2)\right)}\geqslant \log_{5}{(x^2-7x+12)}+\log_{5}{(5-x)}\)
В кредит взяли 220 тыс. рублей на 5 лет под r% годовых. По условиям кредита, на конец первых трех лет задолженность остается неизменной и равной 220 тысячам рублей, а выплаты последних двух лет равны. На конец пятого года кредит должен быть погашен. Найдите r если известно, что сумма всех выплат составит 420 тысяч рублей.