Ежедневные тесты
Меню курса
Декабрь
Беседа ВК для обсуждения тестов: Вступить
Сложность теста - это диапазон сложности задач, которые в этот тест попали. Сложность задачи на сайте - это процент неверных ответов на неё.
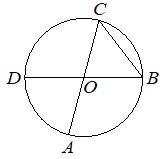
Отрезки AC и BD – диаметры окружности с центром O. Угол ACB равен 59°. Найдите угол AOD. Ответ дайте в градусах.
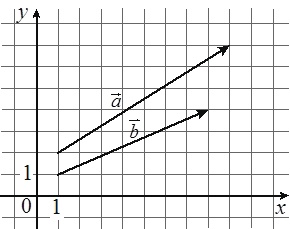
На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\), координатами которых являются целые числа. Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.

На конференцию приехали учёные из трёх стран: 5 из Австрии, 4 из Германии и 6 из Сербии. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что десятым окажется доклад учёного из Сербии.
В коробке 12 синих, 6 красных и 7 зелёных фломастеров. Случайным образом выбирают два фломастера. Найдите вероятность того, что окажутся выбраны один синий и один красный фломастеры.
Найдите корень уравнения \(2^{-4-x}=16\)
Найдите значение выражения \(3\cos2\alpha\), если \(\sin\alpha=0{,}6\)
На рисунке изображен график y=f(x). На оси абсцисс отмечены точки 1, 2, 3, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

Сила тока \(I\) (в А) в электросети вычисляется по закону Ома: \(I=\dfrac{U}{R}\), где \(U\) - напряжение электросети (в В), \(R\) - сопротивление подключаемого электроприбора (в Ом). Электросеть прекращает работать, если сила тока превышает 5 А. Определите, какое наименьшее сопротивление может быть у электроприбора, подключаемого к электросети с напряжением 220 В, чтобы электросеть продолжала работать. Ответ дайте в омах.
Два велосипедиста одновременно отправились в 220-километровый пробег. Первый ехал со скоростью, на 9 км/ч большей, чем скорость второго, и прибыл к финишу на 9 часов раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.
На рисунке изображены графики функций \(f(x)=ax^2+bx+c\) и \(g(x)=kx\), пересекающиеся в точках А и B. Найдите абсциссу точки B.
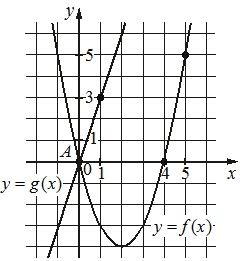
Найдите наименьшее значение функции \(y=9x-9\ln(x+11)+7\) на отрезке [-10,5;0].
а) Решите уравнение \(\cos2x+\sqrt2\cos\left(\dfrac{\pi}2-x\right)-1=0\).
б) Укажите все корни этого уравнения, принадлежащие отрезку \(\left[\dfrac{5\pi}{2}; 4\pi\right]\)
Запишите номера всех верных ответов на пункты а) и б) по возрастанию, через запятую, без пробелов. В первое поле на пункт а), во второе - на пункт б)
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 5π/2 | 18. 8π/3 | 19. 11π/4 | 20. 17π/6 |
| 21. 3π | 22. 19π/6 | 23. 13π/4 | 24. 10π/3 |
| 25. 7π/2 | 26. 11π/3 | 27. 15π/4 | 28. 23π/6 |
| 29. 4π |
Решите неравенство \(3^{x^2}\cdot5^{x-1}\geqslant 3\)
15-го января Егор взял кредит в банке на 15 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что восьмая выплата составила 108 тысяч рублей. Сколько рублей Егор взял в кредит?