Ежедневные тесты
Меню курса
Март
Беседа ВК для обсуждения тестов: Вступить
Сложность теста - это диапазон сложности задач, которые в этот тест попали. Сложность задачи на сайте - это процент неверных ответов на неё.
| 3 | Ежедневный тест 184. Сложность 0-10% |
| 2 | Ежедневный тест 183. Сложность 55-65% |
| 1 | Ежедневный тест 182. Сложность 50-60% |
В треугольнике \(ABC\) угол \(C\) равен 90°, \(BC = 12\), \(\sin{A} = \dfrac{3\sqrt{11}}{10}\). Найдите высоту \(CH\).
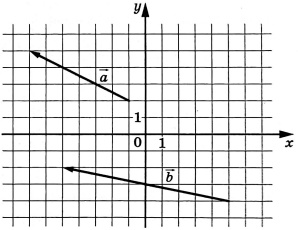
На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\). Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)
Площадь полной поверхности конуса равна 24. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.

В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что сумма выпавших очков равна 16. Результат округлите до тысячных.
На двух линиях выпускают одинаковые лампы. Первая линия выпускает в два раза больше ламп, чем вторая, но вероятность брака на первой линии равна 0,1, а на второй - 0,04. Все лампы поступают на склад. Найдите вероятность того, что случайно выбранная лампа на складе окажется не бракованной.
Найдите наибольший отрицательный корень уравнения \(\cos{\dfrac{(5x-3)\pi}{12}}=-\dfrac{\sqrt3}{2}\).
Найдите значение выражения \((1-\log_515)(1-\log_315)\)
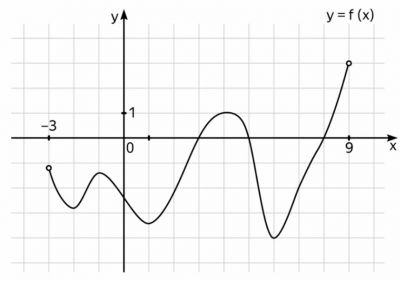
На рисунке изображён график функции \(y=f(x)\), определенной на интервале \((-3;9)\). Найдите количество решений уравнения \(f'(x)=0\) на отрезке \([0;8]\)
На рисунке изображена схема вантового моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами. Введём систему координат: ось \(Oy\) направим вертикально вдоль одного из пилонов, а ось \(Ox\) направим вдоль полотна моста, как показано на рисунке. В этой системе координат линия, по которой провисает цепь моста, имеет уравнение \(y=0{,}001x^2-0{,}28x+26\) где x и y измеряются в метрах. Найдите длину ванты, расположенной в 10 метрах от пилона. Ответ дайте в метрах.

Бригаде из трех рабочих поступил заказ на 120 деталей. Первый рабочий, работая один, выполнит заказ на 2 часа медленнее второго. Третий рабочий делает за час на 4 детали меньше второго. Сколько часов второй и третий рабочий будут выполнять этот заказ, работая вместе, если втроем они выполнят его за 4 часа?
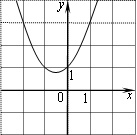
На рисунке изображен график функции вида \(f(x)=ax^2+bx+c\), где \(a\), \(b\) и \(c\) – целые. Найдите значение \(f(-9)\).
Найдите наибольшее значение функции \(y=(x-3)^2(x+6)+9\) на отрезке [-10;0].