Ежедневные тесты
Меню курса
Апрель
Беседа ВК для обсуждения тестов: Вступить
Сложность теста - это диапазон сложности задач, которые в этот тест попали. Сложность задачи на сайте - это процент неверных ответов на неё. Уровень сложности "реального экзамена" примерно 0-40%. Более сложные задачи тоже из ФИПИ, но это редкость. 95+% задач сайта взяты из ФИПИ, сборников Ященко или полностью аналогичны им.
В треугольнике \(ABC\) \(AC=BC=12\), \(\sin B=\dfrac{\sqrt{21}}{5}\). Найдите \(AB\)
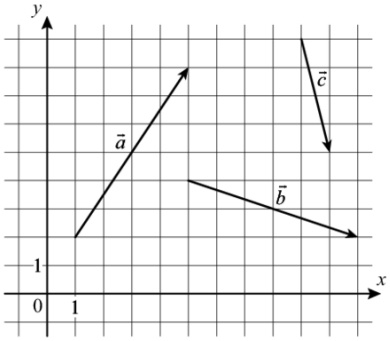
На координатной плоскости изображены векторы \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\). Найдите длину вектора \(\vec{a}+\vec{b}+\vec{c}\)
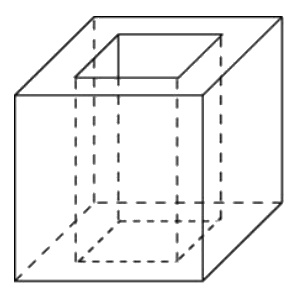
Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,4 и боковым ребром 1. Найдите площадь полной поверхности получившейся фигуры.
Конкурс исполнителей проводится в 4 дня. Всего заявлено 25 выступлений: по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 13 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, то выступление исполнителя из России состоится в последний день конкурса?
В торговом центре два одинаковых автомата с кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,4. Вероятность того, что кофе закончится в обоих автоматах, равна 0,22. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Найдите корень уравнения \(\left(\dfrac14\right)^{1-3x}=2^{x+2}\)
Найдите значение выражения \(\dfrac{3\sin6x}{5\cos3x}\), если \(\sin3x=-0{,}5\)
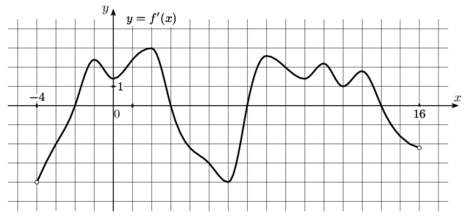
На рисунке изображен график производной функции y=f(x) определенной на интервале (-4;16). Найдите сумму точек экстремума функции f(x).
Высота над землей подброшенного вверх мяча меняется по закону \(h(t)=1{,}4+11t-5t^2\), где \(h\) – высота в метрах, \(t\) – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 7 метров?
Из пункта А круговой трассы, длина которой равна 30 км, одновременно в одном направлении стартовали два автомобилиста. Скорость первого равна 92 км/ч, скорость второго - 77 км/ч. Через сколько минут первый автомобилист будет опережать второго ровно на 1 круг?
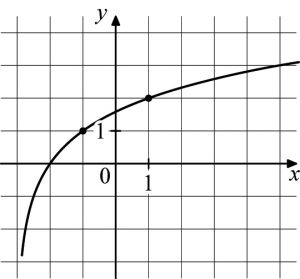
На рисунке изображен график функции \(f(x)=\log_a(x+b)\). Найдите \(f\left(-2,875\right)\).
Найдите точку минимума функции \(y=(3-2x)\cos x+2\sin x+4\), принадлежащую промежутку \(\left(0;\dfrac{\pi}{2}\right)\).
а) Решите уравнение \(\dfrac{4\cos^3x-6\cos x}{\cos\left(2x-\dfrac{\pi}{2}\right)}=3\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[\dfrac{3\pi}2;4\pi\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 3π/2 | 18. 5π/3 | 19. 7π/4 | 20. 11π/6 |
| 21. 2π | 22. 13π/6 | 23. 9π/4 | 24. 7π/3 |
| 25. 5π/2 | 26. 8π/3 | 27. 11π/4 | 28. 17π/6 |
| 29. 3π | 30. 19π/6 | 31. 13π/4 | 32. 10π/3 |
| 33. 7π/2 | 34. 11π/3 | 35. 15π/4 | 36. 23π/6 |
Основанием правильной треугольной пирамиды PABC является треугольник ABC, AP:AB=3:4. На апофеме грани BCP отметили точку K, которая делит эту апофему в отношении 1:4, считая от точки P. Через точки A и K параллельно прямой BC проведена плоскость α.
а) Докажите, что плоскость α перпендикулярна апофеме грани BCP.
б) Найдите угол между прямой AC и плоскостью α.
Решите неравенство \(\dfrac{\log_3(3-x)-\log_3(3x+2)}{\log_3^2x^2+2\log_3x^4+4}\geqslant0\)
В июле 2020 года планируется взять кредит на некоторую сумму. Условия возврата таковы:
— в январе каждого года долг увеличивается на 25% по сравнению с предыдущим годом;
— с февраля по июнь нужно выплатить часть долга одним платежом.
Определите, какую сумму взяли в кредит, если известно, что кредит был выплачен тремя равными платежами (то есть за 3 года) и общая сумма выплат составила 187500 рублей.
Четырёхугольник ABCD вписан в окружность радиуса R=12. Известно, что AB=BC=CD=18.
а) Докажите, что прямые BC и AD параллельны.
б) Найдите AD.
Найдите все значения параметра \(a\), при каждом из которых система уравнений \(\begin{cases}x^4+y^2=a^2\\x^2+y=|a+1|\end{cases}\) имеет ровно четыре решения.
Имеется 8 карточек. На них записывают по одному каждое из чисел -1, 3, 4, -5, 7, -9, -10, 11. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел -1, 3, 4, -5, 7, -9, -10, 11. После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают.
а) Может ли в результате получиться 0?
б) Может ли в результате получиться 1?
в) Какое наименьшее целое неотрицательное число может в результате получиться?
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.