Ежедневные тесты
Меню курса
Сентябрь
Беседа ВК для обсуждения тестов: Вступить
Сложность теста - это диапазон сложности задач, которые в этот тест попали. Сложность задачи на сайте - это процент неверных ответов на неё. 95+% задач сайта взяты из ФИПИ, сборников Ященко или полностью аналогичны им.
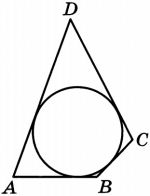
В четырехугольник ABCD вписана окружность, AB=10, CD=17. Найдите периметр четырехугольника ABCD.
Даны векторы \(\vec{a}(-13;4)\) и \(\vec{b}(-6;1)\). Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)
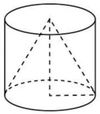
Цилиндр и конус имеют общее основание и высоту. Объём конуса равен 6. Найдите объём цилиндра.
На чемпионате по прыжкам в воду выступают 40 спортсменов, среди них 3 прыгуна из Голландии и 6 прыгунов из Аргентины. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что тринадцатым будет выступать прыгун из Аргентины.
Стрелок стреляет по одному разу в каждую из четырёх мишеней. Вероятность попадания в мишень при каждом отдельном выстреле равна 0,9. Найдите вероятность того, что стрелок попадёт в первую мишень и не попадёт в три последние.
Найдите корень уравнения \(\sqrt{7x-31}=2\)
Найдите значение выражения \(18\sqrt2\mathrm{tg\,}\dfrac{\pi}4\sin\dfrac{\pi}4\)
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.
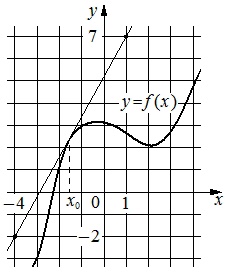
При адиабатическом процессе для идеального газа выполняется закон \(pV^k=6{,}4\cdot10^6\) Па·м⁵, где \(p\) - давление в газе в паскалях, \(V\) - объём газа (в м³), \(k=\frac53\). Найдите, какой объём \(V\) (в м³) будет занимать газ при давлении \(p\), равном \(2 \cdot 10^5\) Па.
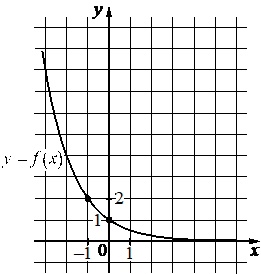
На рисунке изображен график функции вида \(f(x)=a^x\). Найдите значение \(f(-4)\)
Найдите точку максимума функции \(y=x^2-33x+136\ln x+74\)
а) Решите уравнение \(2\log^2_2(2\cos x)-9\log_2(2\cos x)+4=0\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[ -3\pi; -\dfrac{3\pi}{2}\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -3π | 18. -17π/6 | 19. -11π/4 | 20. -8π/3 |
| 21. -5π/2 | 22. -7π/3 | 23. -9π/4 | 24. -13π/6 |
| 25. -2π | 26. -11π/6 | 27. -7π/4 | 28. -5π/3 |
| 29. -3π/2 |
Решите неравенство \(\log_{2}{(18-9x)}-\log_{2}{(x+2)}>\log_{2}{(x^2-6x+8)}\)
В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
- каждый январь долг возрастает на 16% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга, равную 2,523 млн рублей.
Сколько миллионов рублей было взято в банке, если известно, что он был полностью погашен двумя равными платежами (то есть за два года)?