17 вариант ЕГЭ Ященко 2023

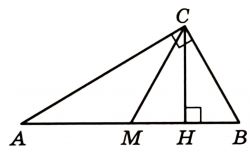
Острый угол B прямоугольного треугольника равен 50°. Найдите угол между высотой CH и медианой CM, проведёнными из вершины прямого угла. Ответ дайте в градусах.

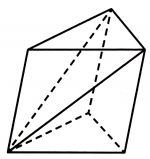
От треугольной призмы, объём которой равен 120, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объём оставшейся части.

Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шашистов, среди которых 3 спортсмена из России, в том числе Василий Лукин. Найдите вероятность того, что в первом туре Василий Лукин будет играть с каким-либо шашистом из России.

Игральный кубик бросают дважды. Известно, что в сумме выпало 6 очков. Найдите вероятность того, что в первый раз выпало 2 очка.

Найдите корень уравнения \(\log_9{3^{2x+9}}=2\).

Найдите значение выражения \(\dfrac{a^{5{,}96}\cdot a^{2{,}4}}{a^{5{,}36}}\) при \(a=6\).

Прямая \(y=5x+11\) является касательной к графику \(y=x^3+4x^2+9x+11\). Найдите абсциссу точки касания.

Расстояние от наблюдателя, находящегося на высоте \(h\) м над землёй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле \(l=\sqrt{\dfrac{Rh}{500}}\), где \(R = 6400\, км\) − радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 24 км. К пляжу ведет лестница, каждая ступенька которой имеет высоту 20 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 32 км?

Первый садовый насос перекачивает 8 литров воды за 4 минуты, второй насос перекачивает тот же объём воды за 6 минут. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 60 литров воды?

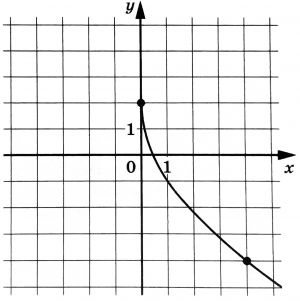
На рисунке изображен график функции \(f(x)=k\sqrt{x}+p\). Найдите значение \(x\), при котором \(f(x)=-10\).

Найдите точку максимума функции \(y=\ln\left(x+25\right)^{11}-11x+5\).

а) Решите уравнение \(5\sin{x}-4\sin^3{x}=2\sin{2x}\).
​б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-\dfrac{7\pi}{2};-2\pi\right] \)

​​Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)

б)

Основание пирамиды SABC — прямоугольный треугольник ABC с прямым углом при вершине C. Высота пирамиды проходит через точку B.
а) Докажите, что середина ребра SA равноудалена от вершин B и C.
б) Найдите угол (в градусах) между плоскостью SBC и прямой, проходящей через середины ребёр BC и SA, если известно, что BS=AC.

Решите неравенство \(\log^2_{2}{\left(x^4\right)}-4\log_{0{,}25}{\left(x^2\right)}\geqslant 12\).

Производство \(x\) тыс. единиц продуктции обходится в \(q=2x^2+5x+10\) млн рублей в год. При цене \(p\) тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет \(px-q\). При каком наименьшем значении \(p\) через 12 лет суммарная прибыль может составить не менее 744 млн рублей при некотором значении \(x\)?

Точки A₁, B₁, C₁ — середины сторон соответственно BC, AC и AB остроугольного треугольника ABC.
а) Докажите, что окружности, описанные около треугольника A₁CB₁, A₁BC₁ и B₁AC₁ пересекаются в одной точке.
б) Известно, что AB = AC = 13 и BC = 10. Найдите радиус окружности, вписанной в треугольник, вершины которого — центры окружностей, описанных около треугольников A₁CB₁, A₁BC₁ и B₁AC₁.

Найдите все значения \(a\), при каждом из которых система уравнений \(\begin{cases} \left(x-2a+2\right)^2+\left(y+a-2\right)^2=a+\dfrac{5}{2}, \\ x+y=1-a \end{cases}\)имеет единственное решение.

Для действительного числа \(x\) обозначим через \(\left[x\right]\) наибольшее целое число, не превосходящее \(x\). Например, \(\left[\dfrac{11}{4}\right]=2\), так как \(2\leqslant\dfrac{11}{4}<3\).
а) Существует ли такое натуральное число \(n\), что \(\left[\dfrac{n}{2}\right]+\left[\dfrac{n}{4}\right]+\left[\dfrac{n}{7}\right]=n\)?
б) Существует ли такое натуральное число \(n\), что \(\left[\dfrac{n}{2}\right]+\left[\dfrac{n}{3}\right]+\left[\dfrac{n}{4}\right]=n+2\)?
в) Сколько существует различных натуральных \(n\), для которых \(\left[\dfrac{n}{2}\right]+\left[\dfrac{n}{3}\right]+\left[\dfrac{n}{9}\right]+\left[\dfrac{n}{17}\right]=n+1945\)?

Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.