36 вариантов ЕГЭ 2023
Меню курса
33 вариант ЕГЭ Ященко 2023
Решение 33 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023
Площадь параллелограмма ABCD равна 145. Найдите площадь параллелограмма A'B'C'D', вершинами которого являются середины сторон данного параллелограмма.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 188. Найдите объём конуса.
Научная конференция проводится в 3 дня. Всего запланировано 50 докладов: в первый день 22 доклада, остальные распределены поровну между вторым и третьим днями. На конференции планируется доклад профессора М. Порядок докладов определяется жеребьёвкой. Какова вероятность того, что доклад профессора М. окажется запланированным на последний день конференции?
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,05. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,05. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Найдите корень уравнения \(\sqrt{11-5x}=1-x\). Если уравнение имеет более одного корня, в ответе запишите наибольший из корней.
Найдите \(\log_{a}{(ab^8)}\), если \(\log_{a}{b}=8\)
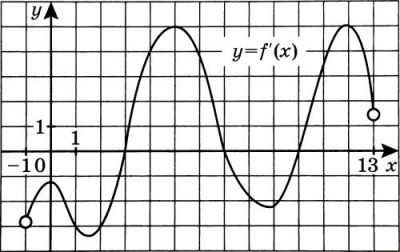
На рисунке изображён график \(y= f'(x)\) — производной функции \(f(x)\), определённой на интервале (-1; 13). Найдите количество точек, в которых касательная к графику функции \(f(x)\) параллельна прямой \(y = x + 18\) или совпадает с ней.
Перед отправкой тепловоз издал гудок с частотой \(f_0=292\, Гц\). Чуть позже гудок издал подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка \(f\) больше первого: она зависит от скорости тепловоза по закону \(f(v)=\dfrac{f_0}{1-\dfrac{v}{c}} (Гц)\), где \(c\) - скорость звука (в м/с).Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее, чем на \(8\, Гц\). Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, a \(c=300\, м/с\). Ответ выразите в м/с.
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 16 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 10 км/ч больше скорости другого?
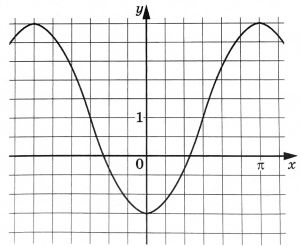
На рисунке изображен график функции \(f(x)=a\cos x+b\). Найдите \(a\).
Найдите наибольшее значение функции \(y=(x^2+22x-22)e^{2-x}\) на отрезке [0;5].
а) Решите уравнение \(\log_{\frac{1}{2}}{(3\cos2x-2\cos^2x+5)}=-2\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[5\pi; \dfrac{13\pi}{2}\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 5π | 18. 31π/6 | 19. 21π/4 | 20. 16π/3 |
| 21. 11π/2 | 22. 17π/3 | 23. 23π/4 | 24. 35π/6 |
| 25. 6π | 26. 37π/6 | 27. 25π/4 | 28. 19π/3 |
| 29. 13π/2 |
В правильной треугольной усечённой пирамиде \(ABCA_1B_1C_1\) площадь нижнего основания \(ABC\) в четыре раза больше площади меньшего основания \(А_1B_1С_1.\) Через ребро \(AC\) проведена плоскость \(\alpha\), которая пересекает ребро \(BB_1\) в точке \(K\) и делит пирамиду на два многогранника равного объёма.
а) Докажите, что точка \(K\) делит ребро \(BB_1\) в отношении \(7:1\), считая от точки \(B\).
б) Найдите площадь сечения усечённой пирамиды плоскостью \(\alpha\), если высота пирамиды равна \(2\sqrt{2}\), а ребро меньшего основания равно \(2\sqrt{6}\).
Решите неравенство \(25^{2x^2-0{,}5}-0{,}6\cdot4^{2x^2+0{,}5}\leqslant10^{2x^2}\)
В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
- каждый январь долг возрастает на 15% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга, равную 1,587 млн рублей.
Сколько миллионов рублей было взято в банке, если известно, что он был полностью погашен двумя равными платежами (то есть за два года)?
Окружность проходит через вершины \(A\), \(B\) и \(D\) параллелограмма \(ABCD\), пересекает сторону \(BC\) в точках \(B\) и \(M\), а также пересекает продолжение стороны \(CD\) за точку \(D\) в точке \(N\).
а) Докажите, что \(AM=AN\).
б) Найдите отношение \(CD:DN\), если \(AB:BC = 1:3\), а \(\cos\angle BAD=0{,}4\).
Ответ запишите в виде несократимого отношения без пробелов, например "4:13".
Найдите все значения параметра a, при которых система уравнений
\(\begin{cases}\dfrac{(\sqrt{12-x^2}-y)\left((x+4)^2+(y+4)^2-8(x+4)+x^2-y^2-24\right)}{2-x^2}=0\\y=1-2a\end{cases}\)
имеет ровно два решения.
В школах № 1 и № 2 учащиеся писали тест. Из каждой школы тест писали по крайней мере 2 учащихся, а суммарно тест писал 51 учащийся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешёл из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах,
а) Мог ли средний балл в школе № 1 вырасти в 2 раза?
б) Средний балл в школе № 1 вырос на 10 %, средний балл в школе № 2 также вырос на 10 %. Мог ли первоначальный средний балл в школе № 2 равняться 1?
в) Средний балл в школе № 1 вырос на 10 %, средний балл в школе № 2 также вырос на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.