36 вариантов ЕГЭ 2023
Меню курса
30 вариант ЕГЭ Ященко 2023
Решение 30 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023
В треугольнике ABC средняя линия DE параллельна стороне AB. Найдите площадь треугольника ABC, если площадь трапеции ABED равна 48.
В цилиндрическом сосуде уровень жидкости достигает 25 см. На какой высоте будет находится уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2,5 раза больше диаметра первого? Ответ дайте в сантиметрах.
В чемпионате по толканию ядра участвуют спортсмены из четырёх стран: 5 из Японии, 4 из Кореи, 9 из Китая и 7 из Индии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется из Индии.
За круглый стол на 6 стульев в случайном порядке рассаживаются 4 мальчика и 2 девочки. Найдите вероятность того, что обе девочки не будут сидеть рядом.
Найдите корень уравнения \((x-11)^4=(x+3)^4 \)
Найдите значение выражения \(\dfrac{(\sqrt{20}+\sqrt{12})^2}{4+\sqrt{15}}\)
Материальная точка движется прямолинейно по закону \(x(t)=\frac{1}{2}t^3-2t^2+6t+25 \), где \(x\) – расстояние от точки отсчёта в метрах, \(t\) - время в секундах, прошедшее с момента начала движения. Найдите её скорость (в метрах в секунду) в момент времени \(t = 4\).
Водолазный колокол, содержащий \(\nu=2\) моля воздуха при давлении \(p_1=2{,}4\) атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления \(p_2\) в атмосферах. Работа, совершаемая водой при сжатии воздуха, вычисляется по формуле \(A=a\nu T\log_{2}{\dfrac{p_2}{p_1}} \), где \(a=13{,}5 \dfrac{Дж}{моль \cdot К}\) - постоянная, \(T=300 \,К\) - температура воздуха. Найдите, какое давление \(p_2\) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в \(16200 Дж\). Ответ дайте в атмосферах.
Первая труба заполняет резервуар объёмом 440 литров на 4 минуты медленнее, чем вторая труба заполняет резервуар объёмом 396 литров. Первая труба пропускает на 2 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба?
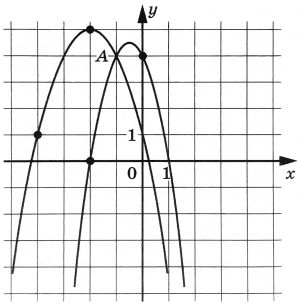
На рисунке изображены графики функций \(f(x)=-2x^2-2x+4\) и \(g(x)=ax^2+bx+c\), которые пересекаются в точках \(A(-1;4)\) и \(B(x_0;y_0)\). Найдите \(x_0\).
Найдите точку минимума функции \(y=(x+8)^2\cdot e^{-x-3} \)
а) Решите уравнение \(\cos{2x}\sin{2x}\sin{\frac{2\pi}{3}}=\dfrac{1}{4}\cos{\left(8x-\frac{3\pi}{2} \right)}\)
б) Укажите корни этого уравнения, принадлежащие отрезку \(\left[\frac{8\pi}{3};\frac{10\pi}{3} \right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. πn/4, n∈Z | 2. π/12+πn/2, n∈Z | 3. 5π/24+πn/2, n∈Z | 4. 3π/8+πn/2, n∈Z |
| 5. -π/12+πn/2, n∈Z | 6. -5π/24+πn/2, n∈Z | 7. -3π/8+πn/2, n∈Z |
б)
| 8. 8π/3 | 9. 65π/24 | 10. 11π/4 | 11. 67π/24 |
| 12. 17π/6 | 13. 23π/8 | 14. 3π | 15. 19π/6 |
| 16. 25π/8 | 17. 77π/24 | 18. 13π/4 | 19. 79π/24 |
| 20. 10π/3 |
Радиус основания конуса равен 12, а высота конуса равна 5.
а) Постройте сечение конуса плоскостью, проходящей через вершину конуса и взаимно перпендикулярные образующие.
б) Найдите расстояние от плоскости сечения до центра основания конуса.
Решите неравенство \(30\cdot 3^{\log_{2}{(7-x)}}+3^{1+\log_{2}{x}}-3^{\log_{2}{(7x-x^2)}}\geqslant 90\)
Бригаду из 30 рабочих нужно распределить по двум объектам. Если на первом объекте работает p человек, то каждый из них получает в сутки 200p руб. Если на втором объекте работает p человек, то каждый из них получает в сутки (50p+300) руб. Как нужно распределить рабочих по объектам, чтобы их суммарная суточная зарплата оказалась наименьшей? Сколько рублей в этом случае придётся заплатить за сутки всем рабочим?
Введите ответ в форме строки "5;15;30000", где на 1 первом месте количество человек на 1 объекте, на 2 месте - на 2 объекте, на 3 месте - наименьшая зарплата.
На сторонах AC, AB, BC прямоугольного треугольника ABC с прямым углом C во внешнюю сторону построены равнобедренные прямоугольные треугольники AKC, ALB и BMC с прямыми углами K, L и M соответственно
а) Докажите, что LC - высота треугольника KLM.
б) Найдите площадь треугольника KLM, если LC=10
Найдите все значения \(a\), при каждом из которых система уравнений \(\begin{cases} \log_{11}{(a - y^2)}=\log_{11}{(a - x^2)}\\x^2+y^2=2x+6y\end{cases} \) имеет ровно два различных решения.
Для набора 40 различных натуральных чисел выполнено, что сумма любых двух чисел из этого набора меньше суммы любых четырёх чисел из этого набора.