36 вариантов ЕГЭ 2023
Меню курса
28 вариант ЕГЭ Ященко 2023
Решение 28 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023
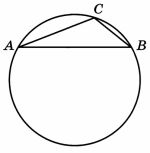
Радиус окружности, описанной около треугольника ABC равен \(2\sqrt{3}\). Найдите AB, если угол ACB равен 120°.
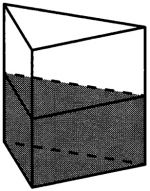
В сосуд, имеющий форму правильной треугольной призмы, налили 1100 см³ воды и полностью в неё погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 29 см. Чему равен объём детали? Ответ выразите в см³.
Симметричную монету подбрасывают трижды. Найдите вероятность того, что "орел" выпадет ровно один раз.
По отзывам покупателей Пётр Петрович оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят вовремя из магазина А, равна 0,92. Вероятность того, что этот товар доставят вовремя из магазина Б, равна 0,85. Пётр Петрович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар вовремя.
Найдите корень уравнения \(\left(\dfrac15\right)^{3x+5} = 0{,}04\).
Найдите значение выражения \(2\sqrt{6}\cos{\dfrac{\pi}{4}}\sin{\dfrac{7\pi}{6}}\mathrm{tg}\left(-\dfrac{2\pi}{3}\right) \).
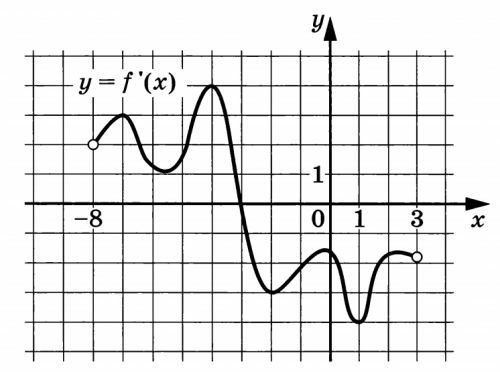
На рисунке изображён график \(y = f’(x)\) – производной функции \(f(x)\), определённой на интервале \((-8; 3)\). В какой точке отрезка \([-5; 0]\) функции \(f(x)\) принимает наибольшее значение?
Независимое агентство намерено ввести рейтинг \(R\) новостных изданий на основе показателей информативности \(In\), оперативности \(Op\) и объективности \(Tr\) публикаций, а также качества \(Q\) сайта. Каждый отдельный показатель – целое число от 0 до 4. Составители рейтинга считают, что информативность публикаций ценится вдвое, а объективность – втрое дороже, чем оперативность и качество сайта, то есть \(R = \dfrac{2In + Op + 3Tr + Q}{A}\). Найдите, каким должно быть число \(A\), чтобы издание, у которого все показатели максимальны, получило рейтинг 1.
Дорога между пунктами A и B состоит из подъёма и спуска, а её длина равна 36 км. Путь из A в B занял у туриста 10 часов, из которых 2 часа ушло на спуск. Найдите скорость туриста на спуске, если она больше скорости на подъёме на 3 км/ч. Ответ дайте в км/ч.
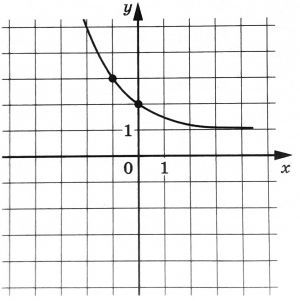
На рисунке изображен график функции \(f(x)=a^x+b\). Найдите, при каком значении \(x\) значение функции равно 33.
Найдите наибольшее значение функции \(y = 7\ln(x+5) - 7x + 10\) на отрезке \([-4{,}5;0]\)
а) Решите уравнение \(\cos2x-\sin2x=\cos x+\sin x+1\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-\dfrac{5\pi}2;-\pi\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4.π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -5π/2 | 18. -7π/3 | 19. -9π/4 | 20. -13π/6 |
| 21. -2π | 22. -11π/6 | 23. -7π/4 | 24. -5π/3 |
| 25. -3π/2 | 26. -4π/3 | 27. -5π/4 | 28. -7π/6 |
| 29. -π |
В правильной четырёхугольной призме \(ABCDA_1B_1C_1D_1\) сторона основания \(AB\) равна \(3\), а боковое ребро \(AA_1\) равно \(\sqrt{3}\). На рёбрах \(C_1D_1\) и \(DD_1\) отмечены соответственно точки \(K\) и \(M\) так, что \(D_1K = KC_1\), а \(DM : MD_1 = 1 : 3\).
а) Докажите, что прямые \(MK\) и \(BK\) перпендикулярны.
б) Найдите угол между плоскостями \(BMK\) и \(ABB_1\).
Решите неравенство \(\lg^4(x^2-4)^2-\lg^2(x^2-4)^4\geqslant192\)
Сергей хочет купить пакет акций быстрорастущей компании. В начале года у Сергея не было денег на покупку акций, а пакет стоил 160000 рублей. В середине каждого месяца Сергей откладывает на покупку пакета акций одну и ту же сумму, а в конце месяца пакет дорожает, но не более чем на 25%. Какую наименьшую сумму нужно откладывать Сергею каждый месяц, чтобы через некоторое время купить желаемый пакет акций?
На сторонах AC, AB и BC прямоугольного треугольника ABC с прямым углом C вне треугольника ABC построены равнобедренные прямоугольные треугольники AKC, ALB и BMC с прямыми углами K, L и M соответственно.
а) Докажите, что LC – высота треугольника KLM.
б) Найдите площадь треугольника KLM, если LC=6.
Найдите, при каких неположительных значениях \(a\) функции \(f(x) = ax^4 + 4x^3 - 3x^2 - 5\) на отрезке \([-2;2]\) имеет две точки максимума.
Для каждого натурального числа \(n\) обозначим через \(n!\) произведение первых \(n\) натуральных чисел \((1! = 1)\).
а) Существует ли такое натуральное число \(n\), что десятичная запись числа \(n!\) оканчивается ровно 10 нулями?
б) Существует ли такое натуральное число \(n\), что десятичная запись числа \(n!\) оканчивается ровно 17 нулями?
в) Сколько существует натуральных чисел \(n\), меньших 75, для каждого из которых десятичная запись числа \(n!\cdot(75-n)!\) оканчивается ровно 17 нулями?
Введите ответ в форме строки "да;нет;1234". Где ответы на пункты разделены ";", и первый ответ с маленькой буквы.