Разборы тем ЕГЭ
Содержание
7. Производная
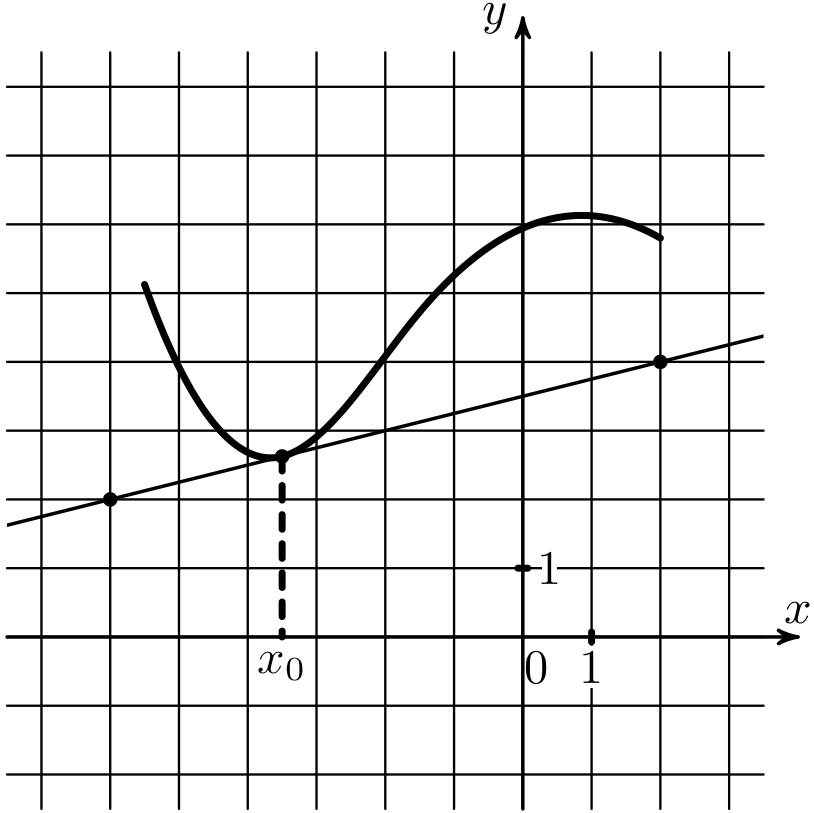
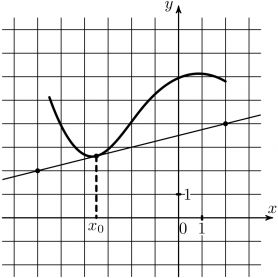
1) На рисунке изображены график функции \(y=f(x)\) и касательная к нему в точке с абсциссой \(x_0\). Найдите значение производной функции \(f(x)\) в точке \(x_0\).
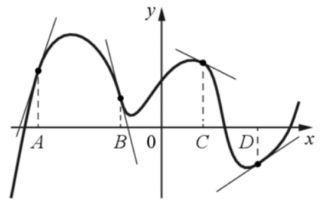
2) На рисунке изображен график функции \( y = f (x)\) и отмечены точки А, В, С и D на оси \(x\). Пользуясь графиком, поставьте в соответствие каждой точке характеристику функции и ее производной.
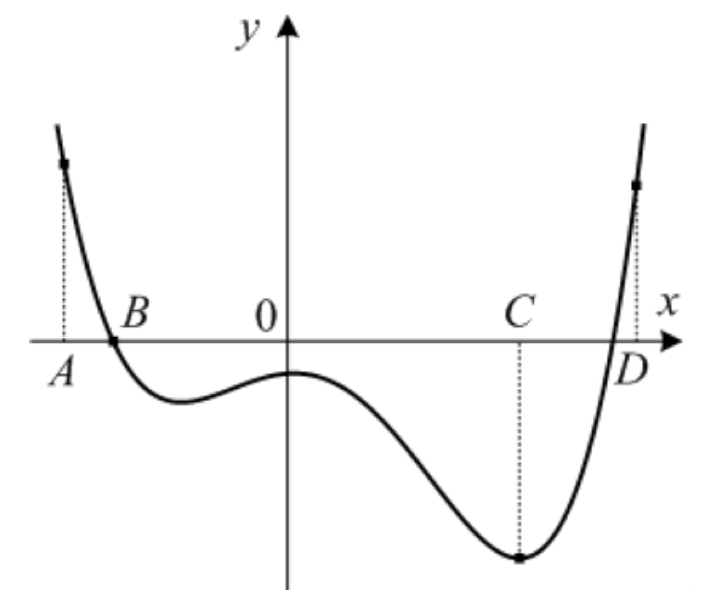
1. Производная равна 0, функция отрицательна;
2. Производная положительна, функция положительна;
3. Производная отрицательна, функция равна 0;
4. Производная отрицательна, функция положительна
3) На рисунке изображены график функции и касательные к нему в точках с абсциссами A, B, C, D. Поставьте в соответствие каждой точке значение производной функции в ней.
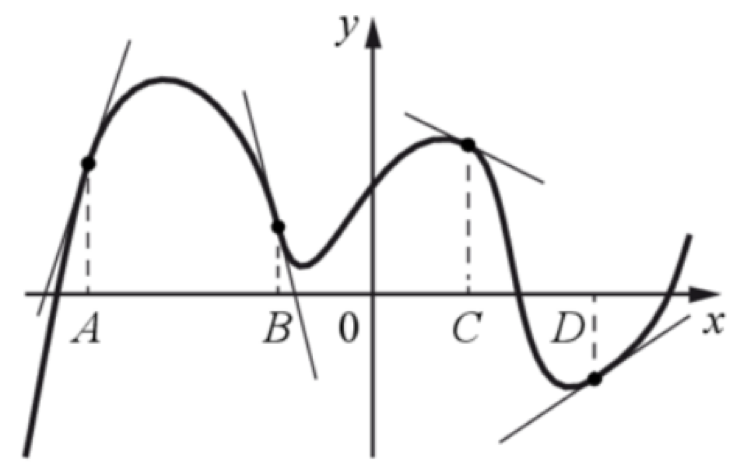
1. -0,5
2. 2/3
3. -4
4. 3
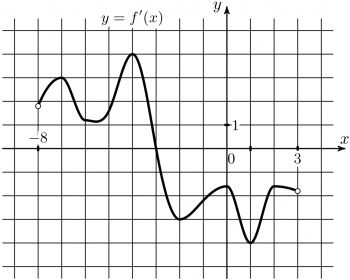
4) На рисунке изображен график производной функции \(y=f(x)\), опрееленной на интервале (-8;3). В какой точке отрезка [-7;-3] функция \(y=f(x)\) принимает наименьшее значение?
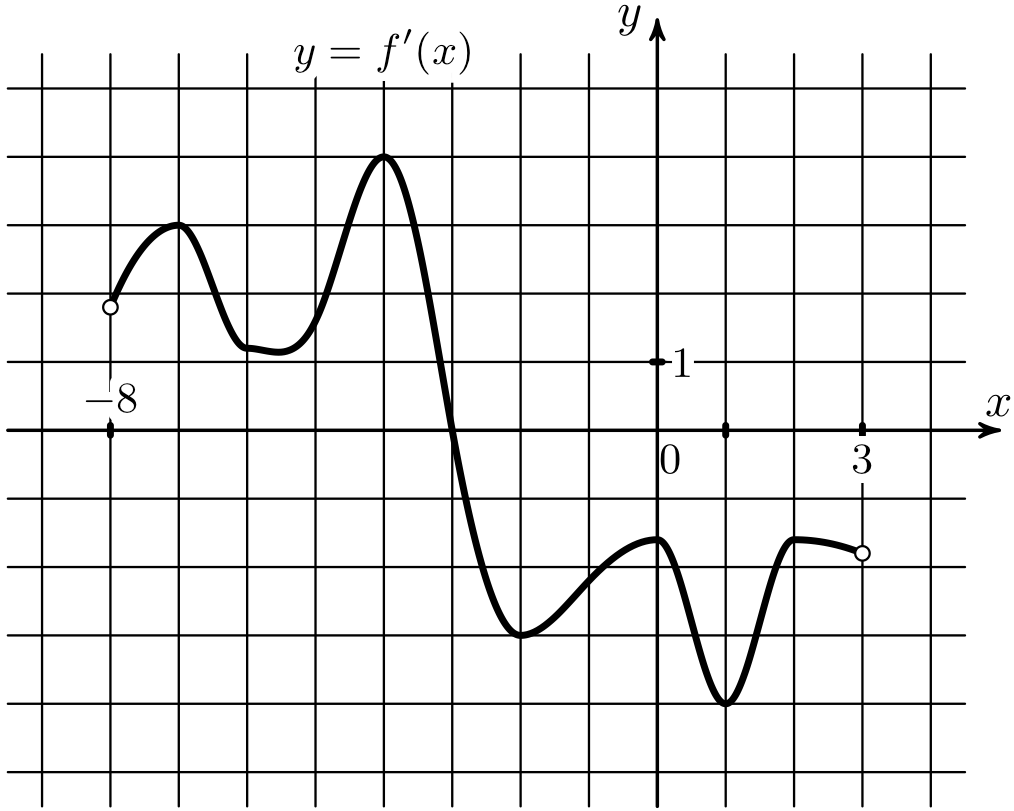
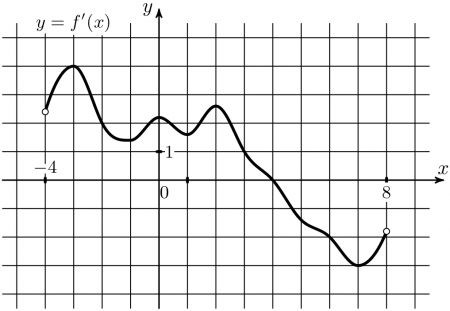
5) На рисунке изображен график \(y=f'(x)\) – производной функции \(y=f(x)\), определенной на интервале (-4;8). Найдите точку экстремума функции \(y=f(x)\), принадлежащую отрезку [-1;7].
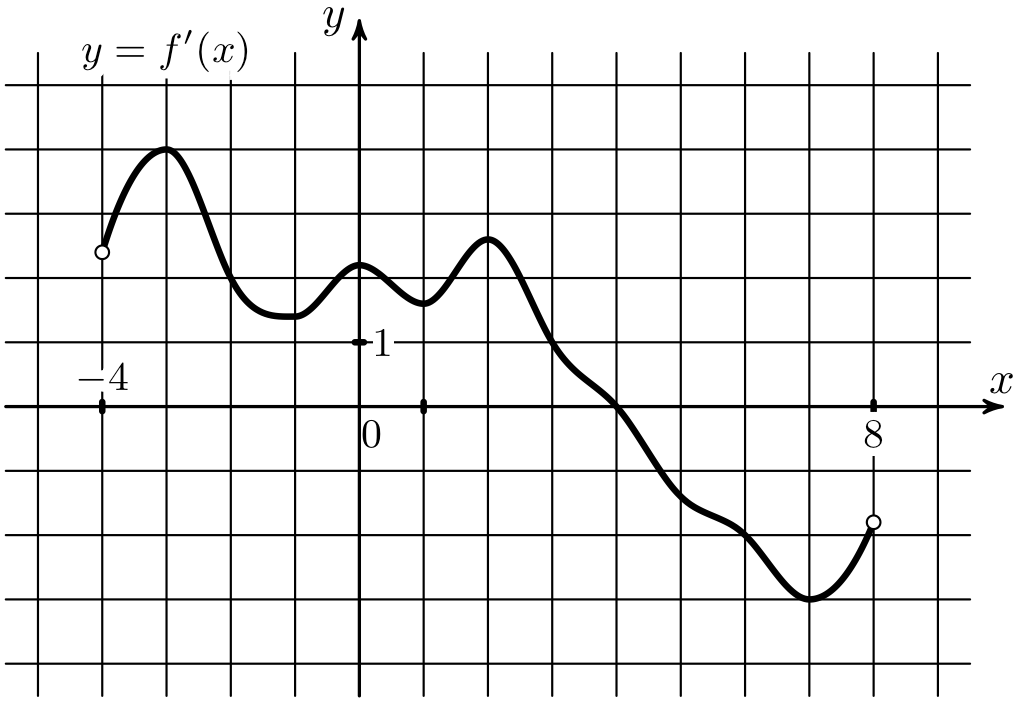
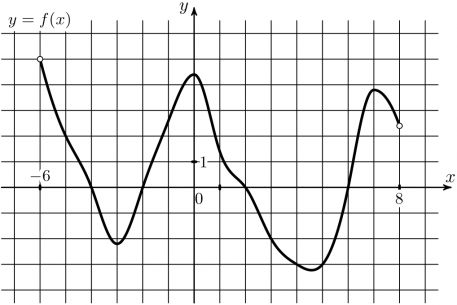
6) На рисунке изображен график \(y=f(x)\). Определите количество целых точек из интервала (-6;8), в которых производная функции \(y=f(x)\) отрицательна.
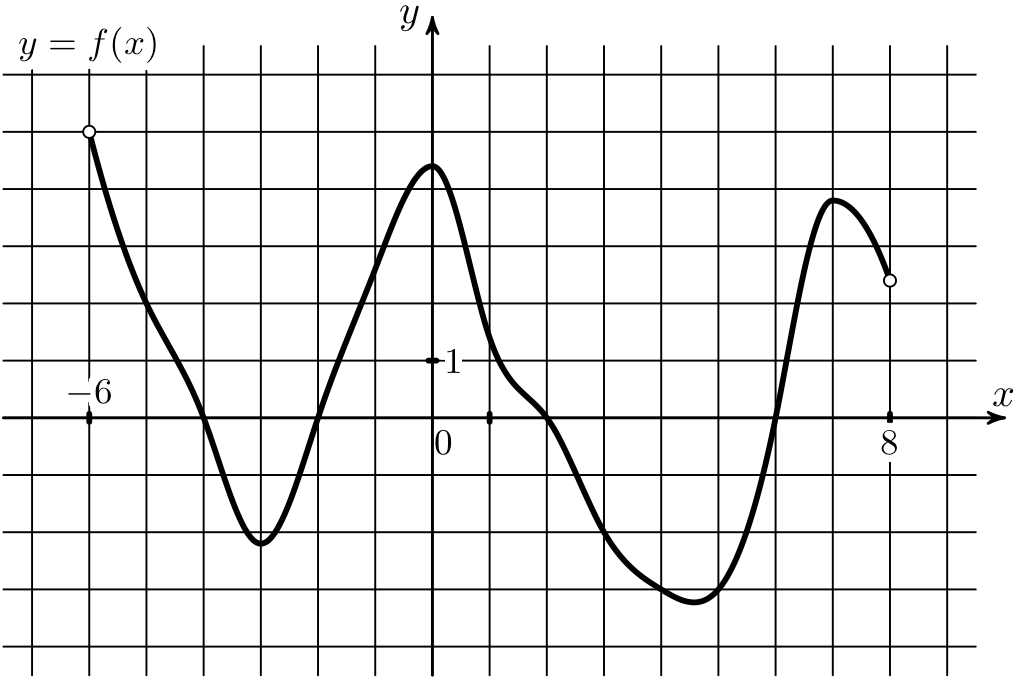
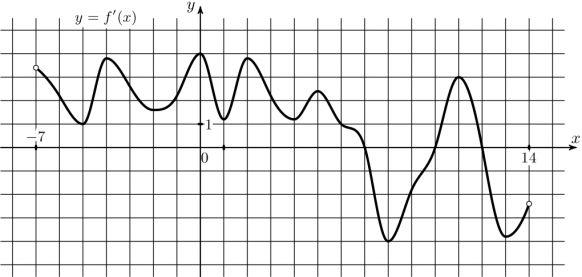
7) На рисунке изображен график функции \(y=f'(x)\) – производной функции \(y=f(x)\), определенной на интервале (-7;14). Найдите количество точке максимума функции \(y=f(x)\), принадлежащих отрезку [-3;13].
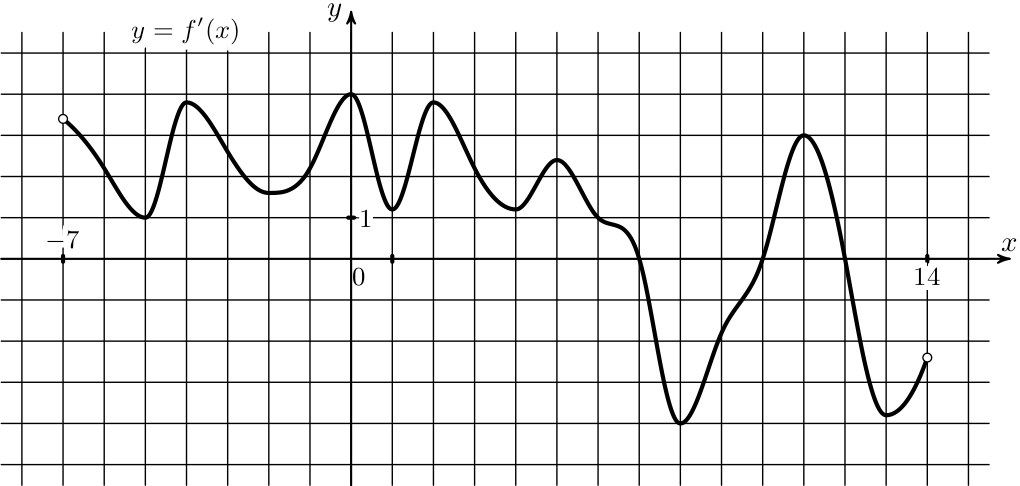
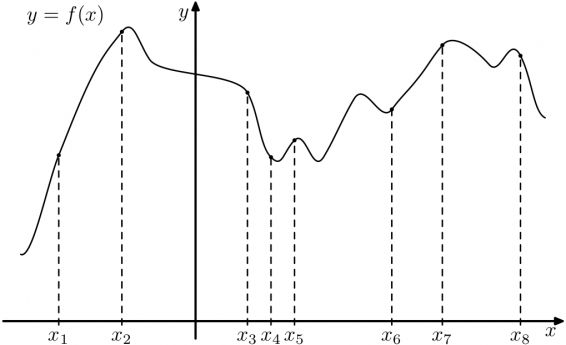
8) На рисунке изображен график функции \(y=f(x)\). На оси абсцисс отмечено восемь точек \(x_1, \ldots, x_8\). Сколько среди этих точек таких, производная в которых отрицательна?
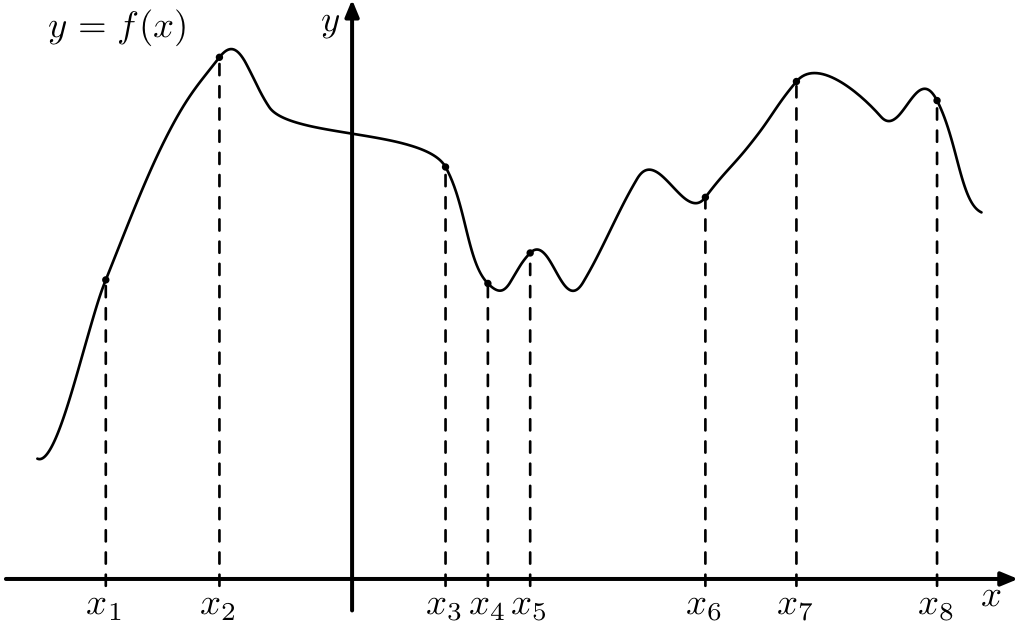
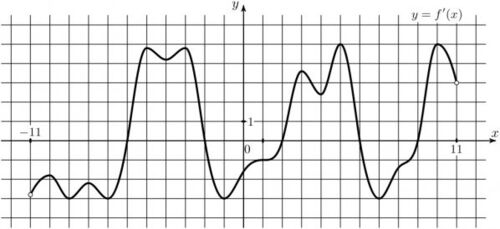
9) На рисунке изображен график производной функции \(y=f(x)\), определенной на интервале (-11;11). Найдите количество точек экстремума, принадлежащих отрезку [-9;10].
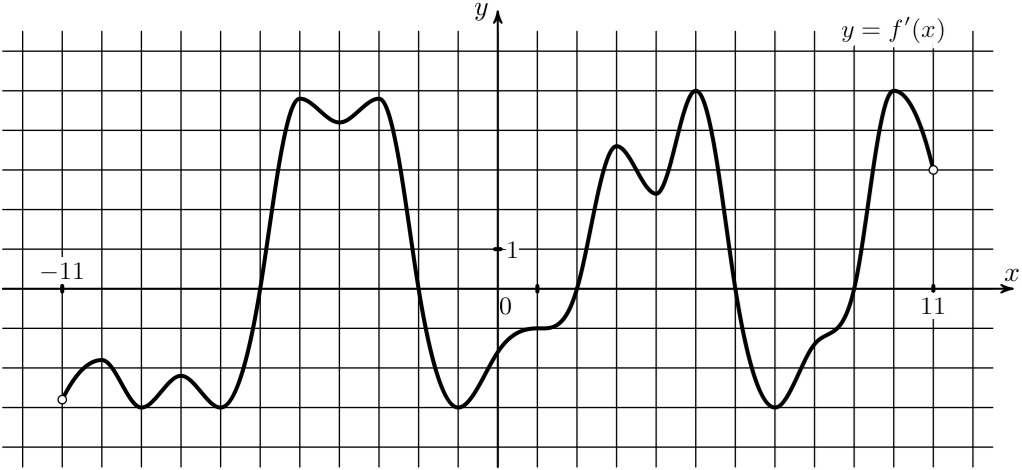
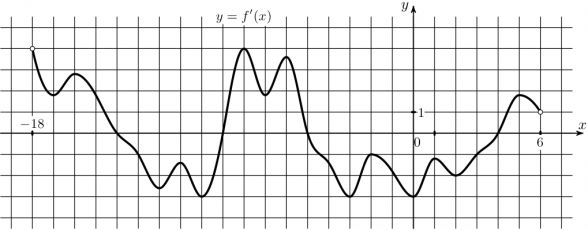
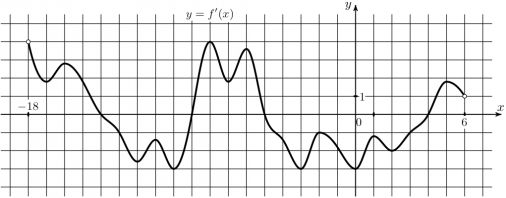
10) На рисунке изображен график производной функции \(y=f(x)\), определенной на интервале (-18;6). Найдите сумму точек экстремума функции \(f(x)\).
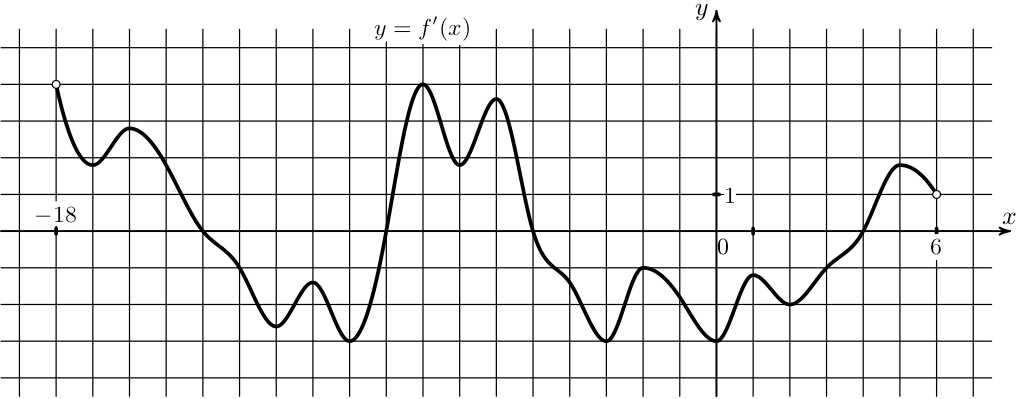
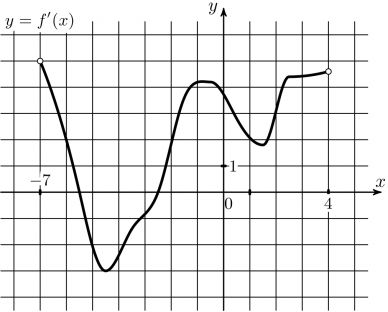
11) На рисунке изображен график производной функции \(y=f(x)\), определенной на интервале (-7;4). Найдите сумму всех целых точек, входящих в промежутки убывания функции \(f(x)\).
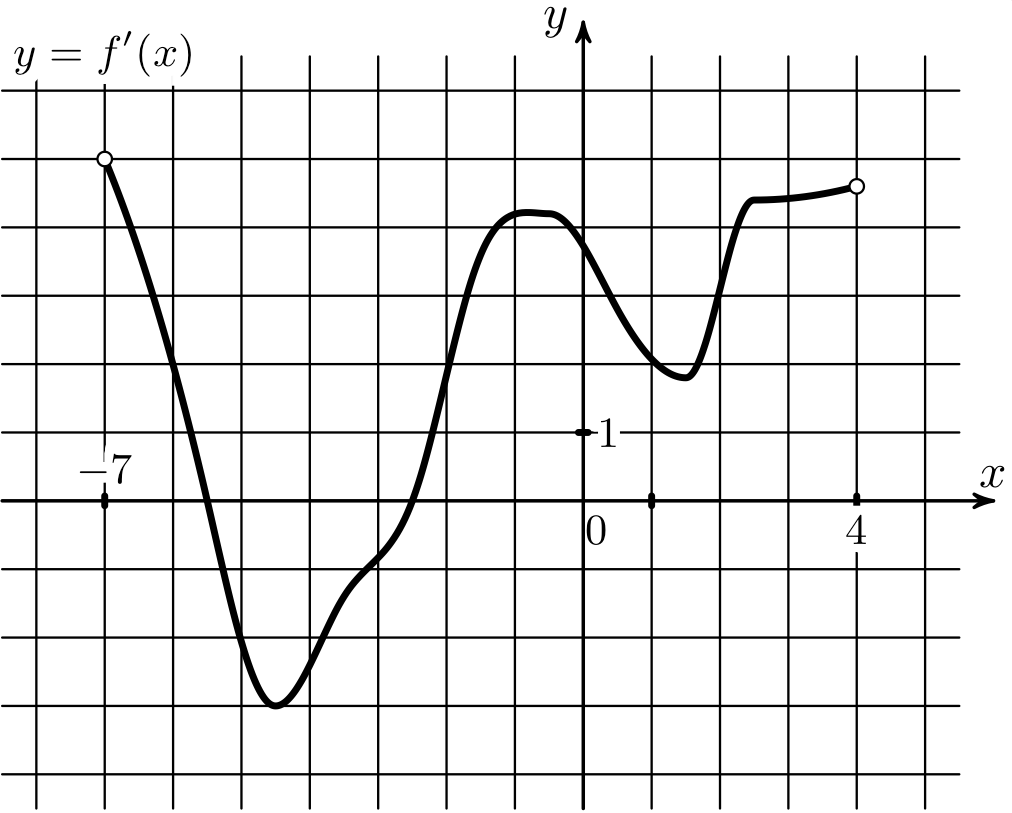
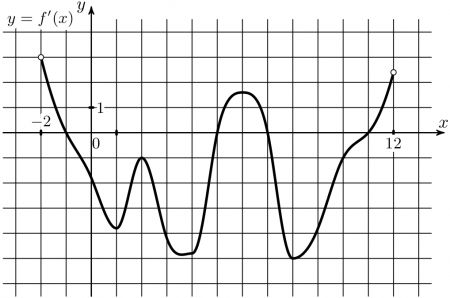
12) На рисунке изображен график производной функции \(y=f(x)\), определенной на интервале (-2;12). Найдите длину наибольшего промежутка возрастания этой функции.
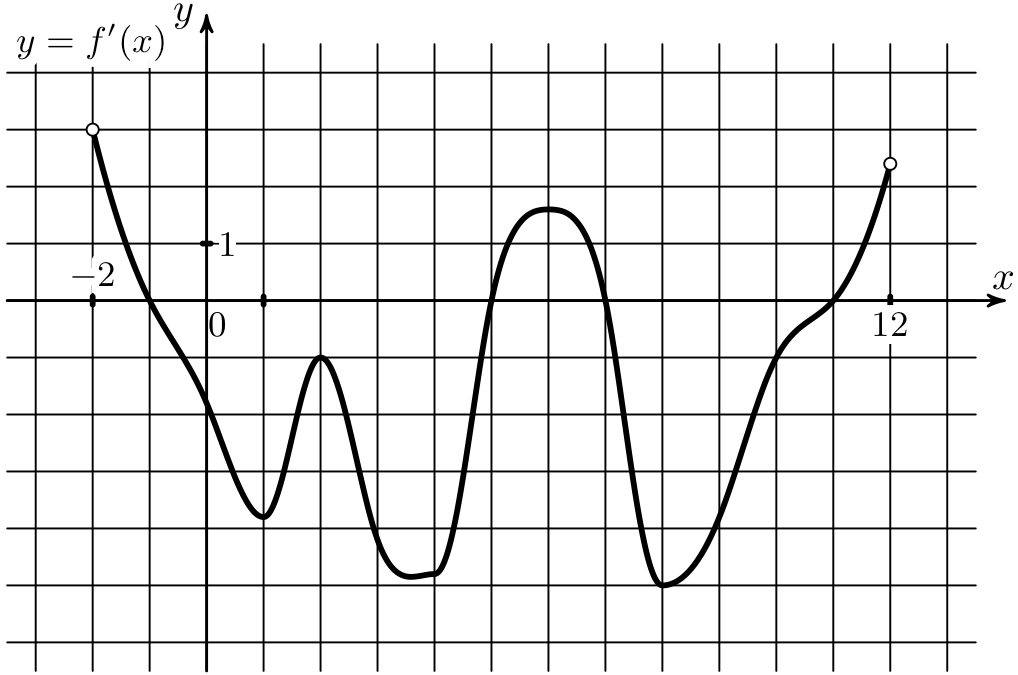
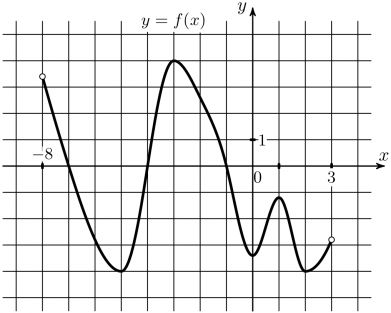
13) На рисунке изобрпжен график функции \(y=f(x)\), определенной на интервале (-8;3). Найдите количество точек, в которых касательная к графику этой функции параллельна прямой \(y=-23\)
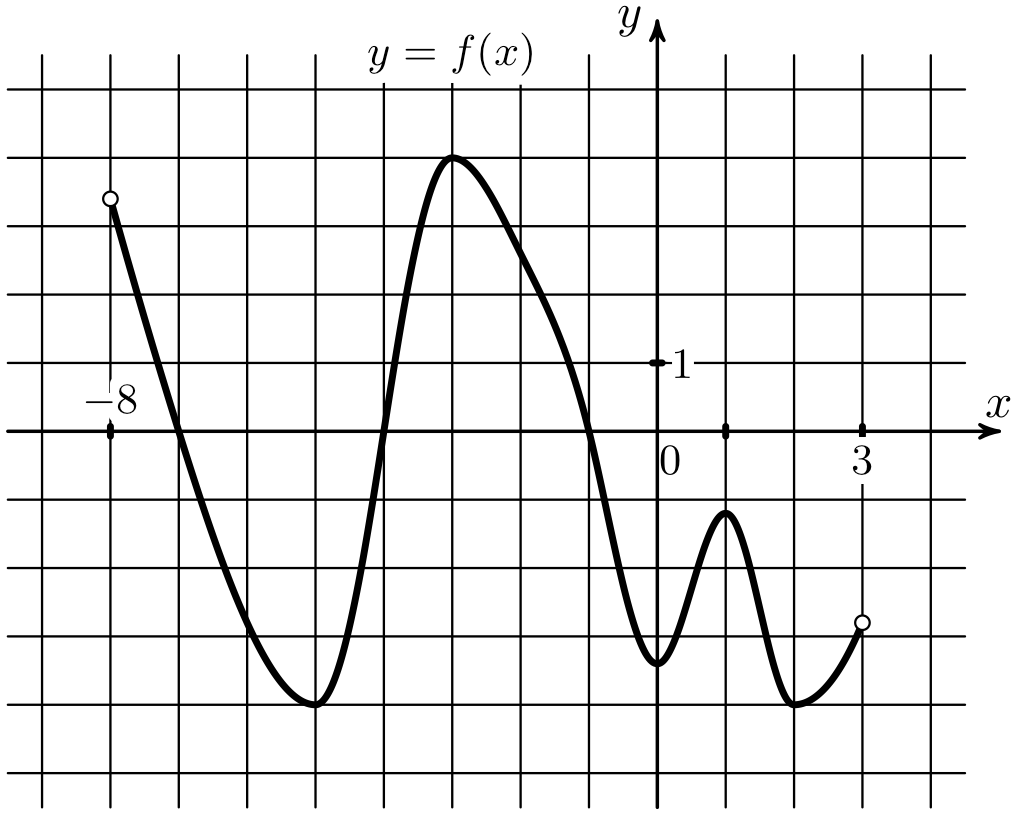
14) На рисунке изображен график производной функции \(y=f(x)\), определенной на интервале (-18;6). Найдите количество точек, в которых касательная к графику функции \(y=f(x)\) параллельна прямой \(y=-9\) или совпадает с ней.
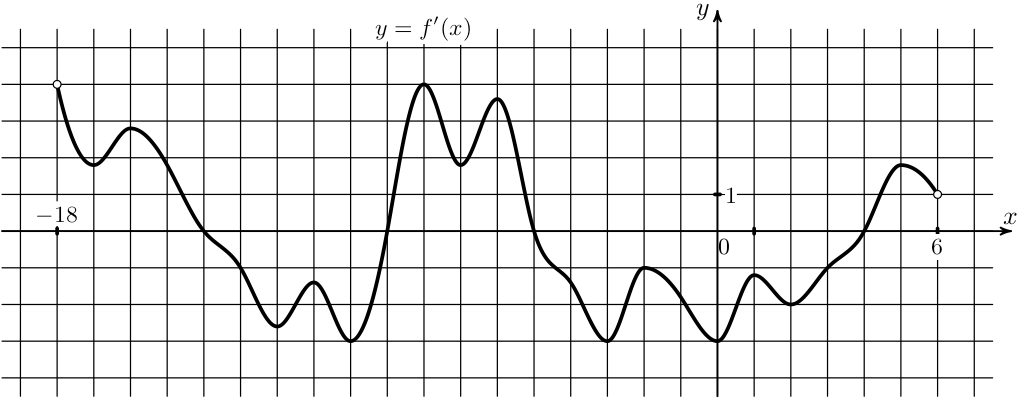
15) На рисунке изображен график производной функции \(y=f(x)\), определенной на интервале (-8;4). Найдите количество точек, в которых касательная к графику функции \(y=f(x)\) параллельна прямой \(y=2x+19\) или совпадает с ней.
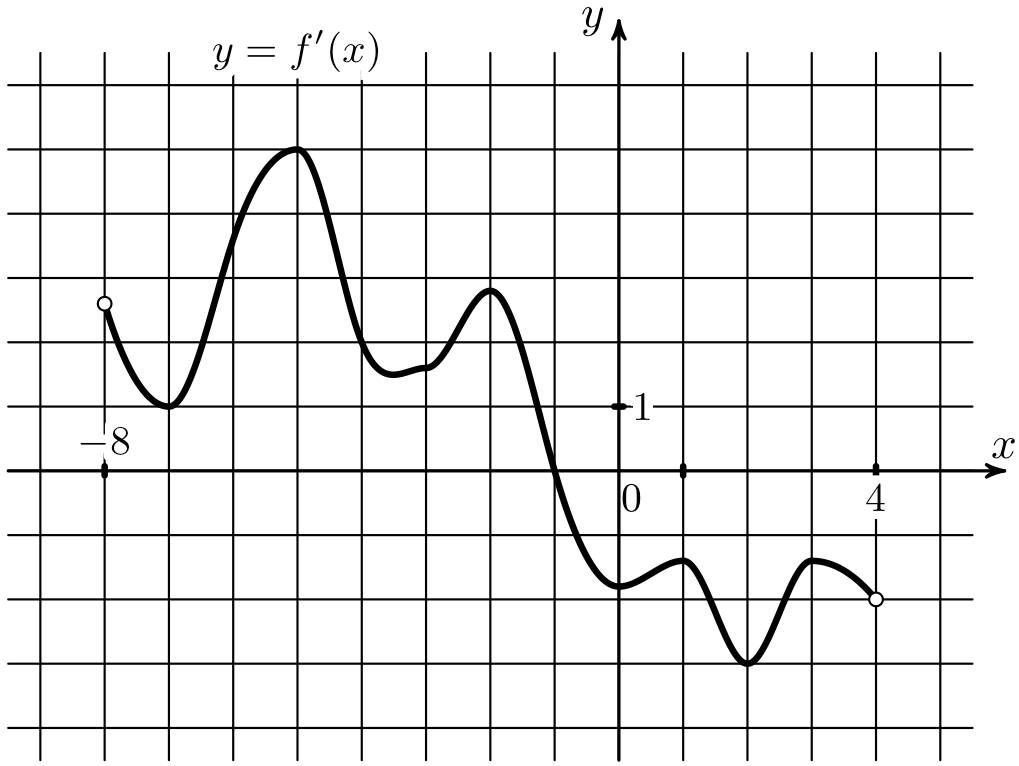
16) На рисунке изображен график производной функции \(y=f(x)\). Найдите абсциссу точки, в которой касательная к графику функции \(y=f(x)\) параллельна прямой \(y=2x+15\) или совпадает с ней.
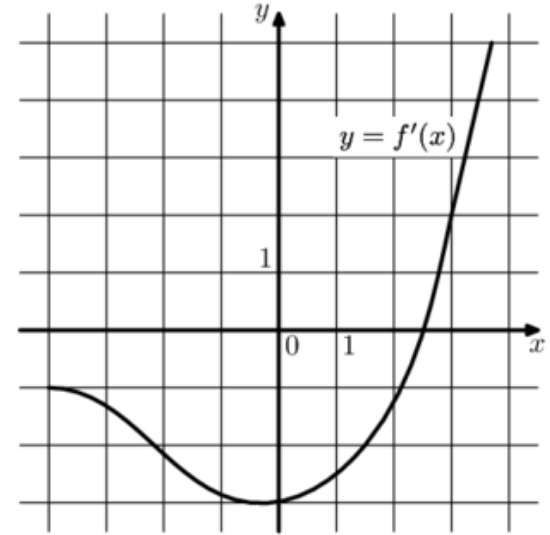
17) Прямая \(y=3x+13\) параллельна касательной к графику функции \(y=x^2-5x+4\). Найдите абсциссу точки касания.
18) Прямая \(y=-6x-2\) касается графика функции \(y=x^3-5x^2+x-5\). Найдите абсциссу точки касания.
19) Прямая \(y=5x-9\) является касательной к графику функции \(f(x)=20x^2-15x+c\). Найдите \(c\).
20) Прямая \(y=-6x-6\) является касательной к графику функции \(f(x)=8x^2+bx+2\). Найдите \(b\), если абсцисса точки касания положительна.
21) Прямая \(y=4x+9\) является касательной к графику функции \(f(x)=ax^2+32x+23\). Найдите \(a\).
22) Материальная точка движется прямолинейно по закону \(x(t)=t^2+7t+3\), где \(x\) – расстояние от точки отсчета в метрах, \(t\) – время в секундах, прошедшее с начала движения. Найдите её скорость (в метрах в секунду) в момент времени \(t=9\) с.
23) Материальная точка движется прямолинейно по закону \(x(t)=-\dfrac14 t^3+4t^2-t+28\), где \(x\) – расстояние от точки отсчета в метрах, \(t\) – время в секундах, прошедшее с начала движения. Найдите её скорость (в метрах в секунду) в момент времени \(t=10\) с.
24) Материальная точка движется прямолинейно по закону \(x(t)=- t^4+5t^3+4t^2-5t-12\), где \(x\) – расстояние от точки отсчета в метрах, \(t\) – время в секундах, прошедшее с начала движения. Найдите её скорость (в метрах в секунду) в момент времени \(t=4\) с.
25) Материальная точка движется прямолинейно по закону \(x(t)=\dfrac16 t^3-8t-16\), где \(x\) – расстояние от точки отсчета в метрах, \(t\) – время в секундах, прошедшее с начала движения. В какой момент времени (в секундах) её скорость была равна 10 м/с?
26) На рисунке изображен график функции \(y=f(x)\), определенный на отрезке (-3;10). Найдите количество решений уравнения \(f'(x)=0\) на отрезке [-1;9].
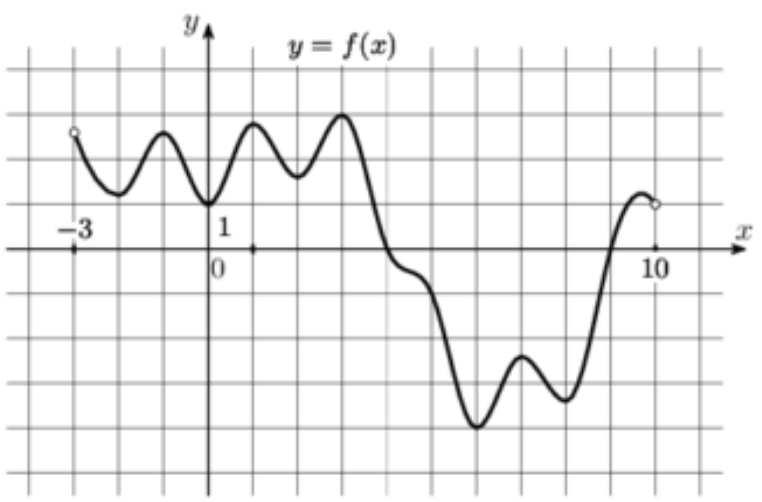
27) На рисунке изображен график функции \(y=F(x)\) – одной из первообразных функции \(f(x)\), определенной на интервале (-2;6). Найдите количество решений уравнения \(f(x)=0\) на отрезке [-1;5].
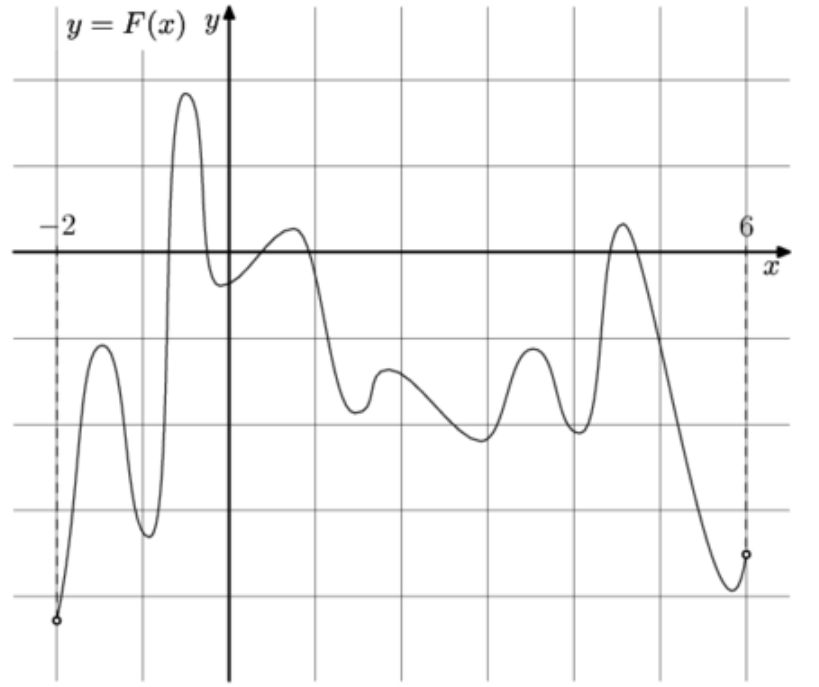
28) На рисунке изображен график функции \(y=f(x)\) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите \(F(6)-F(2)\), где \(F(x)\) – одна из первообразных функции \(f(x)\).
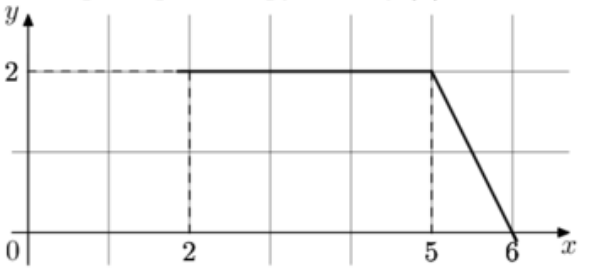
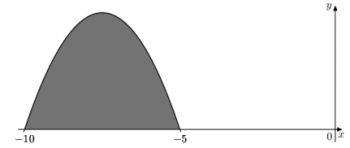
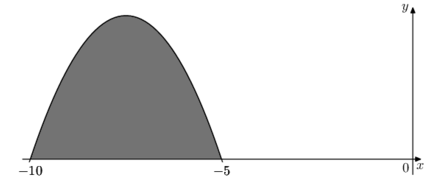
29) На рисунке изображен график некоторой функции \(y=f(x)\). Функция \(F(x)=\dfrac23 x^3+18x^2+163x+\dfrac3{14}\) – одна из первообразных функции \(f(x)\). Найдите площадь закрашенной фигуры.
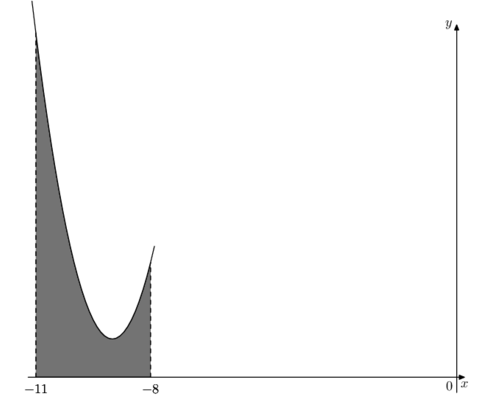
30) На рисунке изображен график некоторой функции \(y=f(x)\). Функция \(F(x)=-\dfrac15 x^3-\dfrac92x^2-30x-\dfrac{12}{17}\) – одна из первообразных функции \(f(x)\). Найдите площадь закрашенной фигуры.
На рисунке изображены график функции \(y=f(x)\) и касательная к нему в точке с абсциссой \(x_0\). Найдите значение производной функции \(f(x)\) в точке \(x_0\).
На рисунке изображен график функции \( y = f (x)\) и отмечены точки А, В, С и D на оси \(x\). Пользуясь графиком, поставьте в соответствие каждой точке характеристику функции и ее производной.
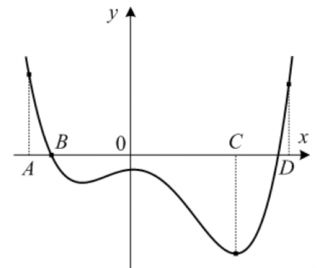
1. Производная равна 0, функция отрицательна;
2. Производная положительна, функция положительна;
3. Производная отрицательна, функция равна 0;
4. Производная отрицательна, функция положительна
На рисунке изображены график функции и касательные к нему в точках с абсциссами A, B, C, D. Поставьте в соответствие каждой точке значение производной функции в ней.
1. -0,5
2. 2/3
3. -4
4. 3
На рисунке изображен график производной функции \(y=f(x)\), определенной на интервале (-8;3). В какой точке отрезка [-7;-3] функция \(y=f(x)\) принимает наименьшее значение?
На рисунке изображен график \(y=f'(x)\) – производной функции \(y=f(x)\), определенной на интервале (-4;8). Найдите точку экстремума функции \(y=f(x)\), принадлежащую отрезку [-1;7].
На рисунке изображен график \(y=f(x)\). Определите количество целых точек из интервала (-6;8), в которых производная функции \(y=f(x)\) отрицательна.
На рисунке изображен график функции \(y=f'(x)\) – производной функции \(y=f(x)\), определенной на интервале (-7;14). Найдите количество точек максимума функции \(y=f(x)\), принадлежащих отрезку [-3;13].
На рисунке изображен график функции \(y=f(x)\). На оси абсцисс отмечено восемь точек \(x_1, \ldots, x_8\). Сколько среди этих точек таких, производная в которых отрицательна?
На рисунке изображен график производной функции \(y=f(x)\), определенной на интервале (-11;11). Найдите количество точек экстремума, принадлежащих отрезку [-9;10].
На рисунке изображен график производной функции \(y=f(x)\), определенной на интервале (-18;6). Найдите сумму точек экстремума функции \(f(x)\).
На рисунке изображен график производной функции \(y=f(x)\), определенной на интервале (-7;4). Найдите сумму всех целых точек, входящих в промежутки убывания функции \(f(x)\).
На рисунке изображен график производной функции \(y=f(x)\), определенной на интервале (-2;12). Найдите длину наибольшего промежутка возрастания этой функции.
На рисунке изображен график функции \(y=f(x)\), определенной на интервале (-8;3). Найдите количество точек, в которых касательная к графику этой функции параллельна прямой \(y=-23\)
На рисунке изображен график производной функции \(y=f(x)\), определенной на интервале (-18;6). Найдите количество точек, в которых касательная к графику функции \(y=f(x)\) параллельна прямой \(y=-9\) или совпадает с ней.
На рисунке изображен график производной функции \(y=f(x)\), определенной на интервале (-8;4). Найдите количество точек, в которых касательная к графику функции \(y=f(x)\) параллельна прямой \(y=2x+19\) или совпадает с ней.
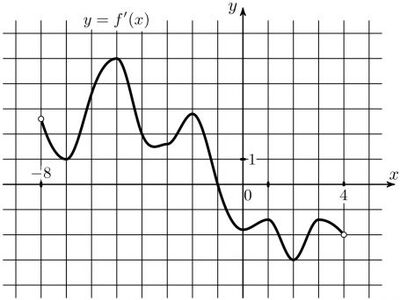
На рисунке изображен график производной функции \(y=f(x)\). Найдите абсциссу точки, в которой касательная к графику функции \(y=f(x)\) параллельна прямой \(y=2x+15\) или совпадает с ней.
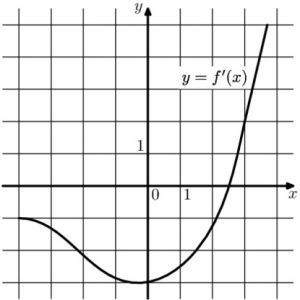
Прямая \(y=3x+13\) параллельна касательной к графику функции \(y=x^2-5x+4\). Найдите абсциссу точки касания.
Прямая \(y=-6x-2\) касается графика функции \(y=x^3-5x^2+x-5\). Найдите абсциссу точки касания.
Прямая \(y=5x-9\) является касательной к графику функции \(f(x)=20x^2-15x+c\). Найдите \(c\).
Прямая \(y=-6x-6\) является касательной к графику функции \(f(x)=8x^2+bx+2\). Найдите \(b\), если абсцисса точки касания положительна.
Прямая \(y=4x+9\) является касательной к графику функции \(f(x)=ax^2+32x+23\). Найдите \(a\).
Материальная точка движется прямолинейно по закону \(x(t)=t^2+7t+3\), где \(x\) – расстояние от точки отсчета в метрах, \(t\) – время в секундах, прошедшее с начала движения. Найдите её скорость (в метрах в секунду) в момент времени \(t=9\) с.
Материальная точка движется прямолинейно по закону \(x(t)=-\dfrac14 t^3+4t^2-t+28\), где \(x\) – расстояние от точки отсчета в метрах, \(t\) – время в секундах, прошедшее с начала движения. Найдите её скорость (в метрах в секунду) в момент времени \(t=10\) с.
Материальная точка движется прямолинейно по закону \(x(t)=-t^4+5t^3+4t^2-5t-12\), где \(x\) – расстояние от точки отсчета в метрах, \(t\) – время в секундах, прошедшее с начала движения. Найдите её скорость (в метрах в секунду) в момент времени \(t=4\) с.
Материальная точка движется прямолинейно по закону \(x(t)=\dfrac16 t^3-8t-16\), где \(x\) – расстояние от точки отсчета в метрах, \(t\) – время в секундах, прошедшее с начала движения. В какой момент времени (в секундах) её скорость была равна 10 м/с?
На рисунке изображен график функции \(y=f(x)\), определенный на интервале (-3;10). Найдите количество решений уравнения \(f'(x)=0\) на отрезке [-1;9].
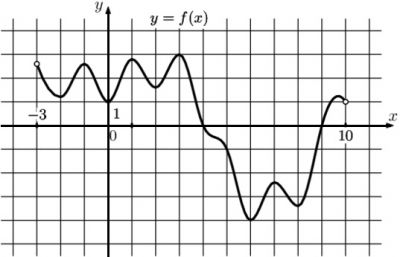
На рисунке изображен график функции \(y=F(x)\) – одной из первообразных функции \(f(x)\), определенной на интервале (-2;6). Найдите количество решений уравнения \(f(x)=0\) на отрезке [-1;5].
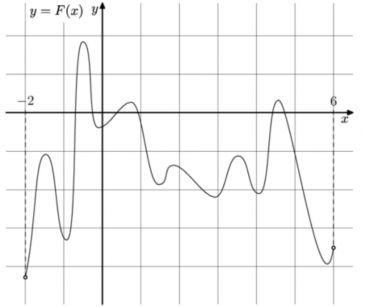
На рисунке изображен график функции \(y=f(x)\) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите \(F(6)-F(2)\), где \(F(x)\) – одна из первообразных функции \(f(x)\).
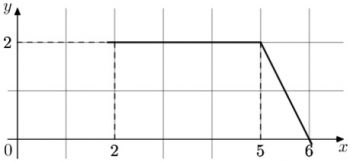
На рисунке изображен график некоторой функции \(y=f(x)\). Функция \(F(x)=\dfrac23 x^3+18x^2+163x+\dfrac3{14}\) – одна из первообразных функции \(f(x)\). Найдите площадь закрашенной фигуры.
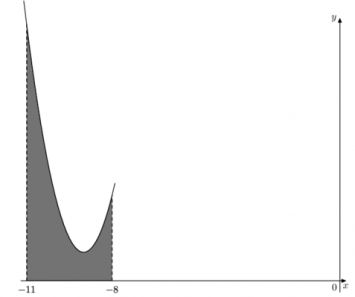
На рисунке изображен график некоторой функции \(y=f(x)\). Функция \(F(x)=-\dfrac15 x^3-\dfrac92x^2-30x-\dfrac{12}{17}\) – одна из первообразных функции \(f(x)\). Найдите площадь закрашенной фигуры.