Реальные варианты ЕГЭ
Меню курса
Основная волна ЕГЭ (27.05.2025)
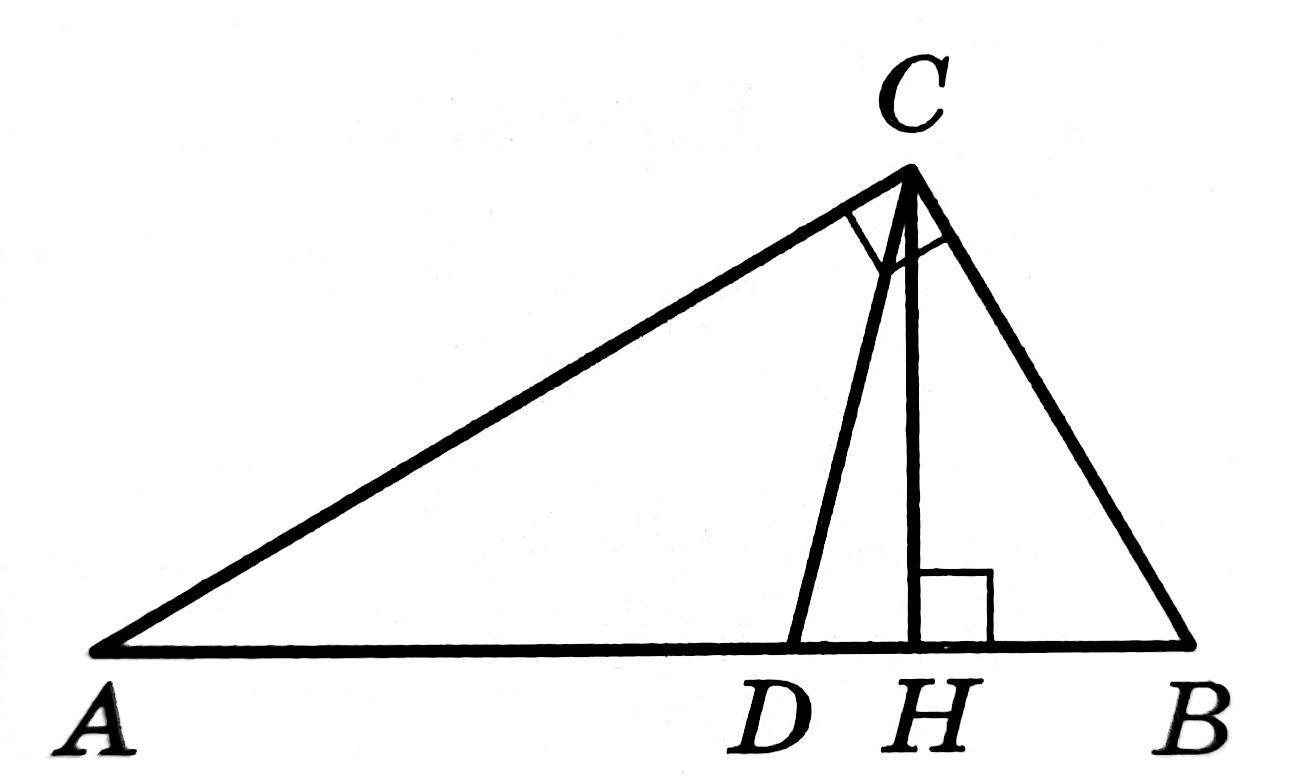
Острый угол B прямоугольного треугольника ABC равен 67°. Найдите угол между высотой CH и биссектрисой CD, проведёнными из вершины прямого угла. Ответ дайте в градусах.
Даны векторы \(\vec{a}(-3;5)\) и \(\vec{b}(1;13)\). Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен 51√2. Найдите образующую конуса.
На олимпиаде по физике 400 участников собираются разместить в четырёх аудиториях: в трёх – по 110 человек, а оставшихся – в запасной аудитории в другом корпусе. Найдите вероятность того, что случайно выбранный участник будет писать олимпиаду в запасной аудитории.
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в первом автомате закончится кофе, равна 0,1. Вероятность того, что кофе закончится во втором автомате, такая же. Вероятность того, что кофе закончится в обоих автоматах, равна 0,03. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решите уравнение \(4^{x-3}=64\)
Вычислите \(\dfrac{\log_{49}16}{\log_7{16}}\)
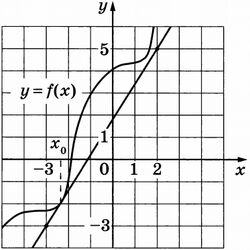
На рисунке изображены график функции \(y=f(x)\) и касательная к нему в точке с абсциссой \(x_0\). Найдите значение производной функции \(f(x)\) в точке \(x_0\).
Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением \(a\) км/ч². Скорость вычисляется по формуле \(v=\sqrt{2la}\), где \(l\) — пройденный автомобилем путь. Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав 0,9 км, приобрести скорость 150 км/ч. Ответ выразите в км/ч².
От пристани A к пристани B, расстояние между которыми равно 420 км, отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним, со скоростью на 1 км/ч большей, отправился второй. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно. Ответ дайте в км/ч.
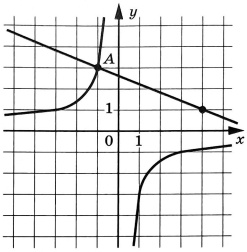
На рисунке изображены графики функций \(f(x)=\dfrac{k}{x}\) и \(g(x)=ax+b\), которые пересекаются в точках A и B. Найдите абсциссу точки B.
Найдите точку максимума функции \(y=x^{3}+18x^{2}+81x+23\).
а) Решите уравнение \(2\sin(-x)+2\sqrt3\sin x-4\cos^2x=\sqrt3-4\)
б) Найдите все корни этого уравнения, принадлежащие промежутку \(\left[2\pi;\dfrac{7\pi}{2}\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 2π | 18. 13π/6 | 19. 9π/4 | 20. 7π/3 |
| 21. 5π/2 | 22. 8π/3 | 23. 11π/4 | 24. 17π/6 |
| 25. 3π | 26. 19π/6 | 27. 13π/4 | 28. 10π/3 |
| 29. 7π/2 |
Решите неравенство \(\dfrac{2^{3x}-10\cdot4^x+17\cdot2^x-8}{x}\geqslant0\)
В июле планируется взять кредит в банке на сумму 14 млн рублей на некоторое целое число лет. Условия его возврата таковы:
– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплачивать часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет взят кредит, если известно, что общая сумма выплат после его погашения равнялась 24,5 млн рублей?