Досрок ЕГЭ 2017

В квартире установлен счётчик холодной воды. Показания 1 марта 270 куб.м., а 1 апреля - 320 куб.м. Сколько нужно заплатить за холодную воду за март, если стоимость 1 куб.м. воды равна 14 руб. 50 коп.?

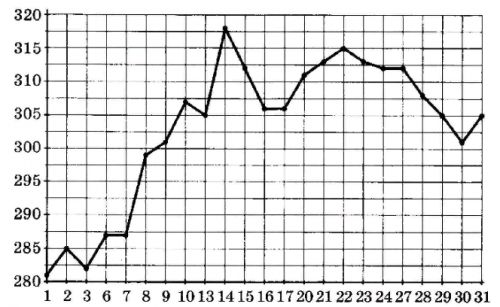
На рисунке жирными точками показана цена палладия на момент закрытия торгов. По горизонтали указываются числа месяца, по вертикали - цена палладия в рублях за грамм. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку максимальную стоимость металла во второй половине месяца.

На клетчатой бумаге с размером клетки 1×1 изображён четырехугольник. Найдите радиус окружности, которую можно вписать в данный четырёхугольник.

Перед началом футбольного матча капитаны команд подбрасывают монету. Какова вероятность того, что команда «Статор» будет начинать все три матча?

Найдите корень уравнения \(\log_{7}{(5x - 3)} = 2\log_{7}{3}\)

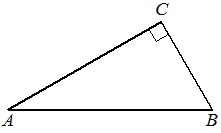
В треугольнике \(ABC\) угол \(C\) равен 90°, \(AB = 10\), \(BC = \sqrt{19}\). Найдите \(\cos A\)

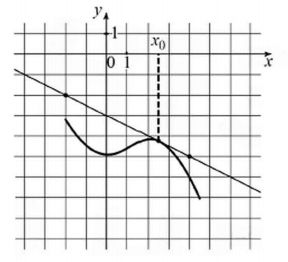
На рисунке изображены график функции \(y = f(x)\) и касательная к нему в точке с абсциссой \(x_0\). Найдите значение производной функции \(f(x)\) в точке \(x_0\).

Дан прямоугольный параллелепипед \(ABCDA_1B_1C_1D_1\). Известно, что \(AA_1 = 5\), \(BC = 4\), \(D_1C_1 = 3\). Найдите объём многогранника \(ADA_1B_1C_1D_1\)

Найдите значение выражения \(\cfrac{\sqrt[3]{36} \cdot \sqrt[5]{36}}{\sqrt[30]{36}}\)

Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы: \(T(t) = T_0 + bt + at^2\), где \(t\) - время в минутах, \(T_0 = 1400\) К, \(a = -10\) К/мин, \(b = 200\) К/мин. Известно, что при температуре нагревателя свыше 1760 К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.

Первый час автомобиль ехал со скоростью 60 км/ч, затем 2 часа со скоростью 110 км/ч, а следующие 2 часа со скоростью 120 км/ч. Найдите среднюю скорость автомобиля на всем пути. Ответ выразите в км/ч.

Найдите наименьшее значение функции \(y = 6\cos{x} + \dfrac{24x}{\pi} + 5\) на промежутке \(\left[-\dfrac{2\pi}{3}; 0\right]\).

а) Решите уравнение \(27^x - 4 \cdot 3^{x+2} + 3^{5-x} = 0\)
б) Укажите корни этого уравнения, принадлежащие отрезку \([\log_{7}{4};\log_{7}{16}]\)

В ответ запишите корни без пробелов через точку с запятой в порядке возрастания. Сначала на пункт а, затем на пункт б. Например, "8;13;8"

Найдите все значение параметра \(a\), при каждом из которых система неравенств \(\begin{cases} ax \geqslant 2\\\sqrt{x - 1} > a\\3x \leqslant 2a+11 \end{cases}\) имеет хотя бы одно решение на отрезке \(x \in [3;4]\).