Досрок ЕГЭ по математике профиль 2025

Площадь параллелограмма ABCD равна 12. Точка Е - середина стороны AD. Найдите площадь трапеции BCDE.

​

Даны векторы \(\vec{a}(5;2)\) и \(\vec{b}(3;-6)\). Найдите скалярное произведение векторов \(\vec{a}-\vec{b}\) и \(5\vec{a}-\vec{b}\)

Цилиндр вписан в правильную четырехугольную призму. Радиус основания и высота цилиндра равны 5. Найдите объем призмы.

Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд будет начинать игру. Команда "Сапфир" играет три матча с разными командами. Найдите вероятность того, что в этих матчах команда "Сапфир" начнёт только последнюю игру.

Помещение освещается тремя лампами. Вероятность перегорания каждой лампы в течение года равна 0,4. Лампы перегорают независимо друг от друга. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.

Найдите корень уравнения \(\log_7(4-x)=2\)

Найдите значение выражения \( 5\cos2\alpha\), если \(\sin\alpha=-0{,}9\)

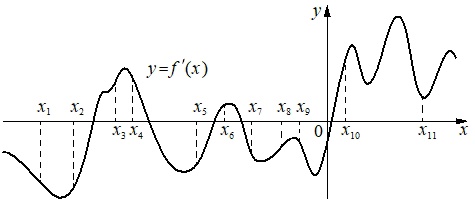
На рисунке изображен график функции y=f’(x) - производной функции y=f(x) и одиннадцать точек на оси абсцисс: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁. Сколько из этих точек принадлежит промежуткам убывания функции f(x)?

​

Мотоциклист, движущийся по городу со скоростью \(v_0=57\)км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением \(a=8\)км/ч². Расстояние (в км) от мотоциклиста до города вычисляется по формуле \(S=v_0 t+\dfrac{a t^2}{2}\), где \(t\) - время в часах, прошедшее после выезда из города. Определите время, прошедшее после выезда мотоциклиста из города, если известно, что за это время он удалился от города на 45 км. Ответ дайте в минутах.

Один мастер может выполнить заказ за 15 часов, а другой — за 10 часов. За сколько часов выполнят этот заказ оба мастера, работая вместе?

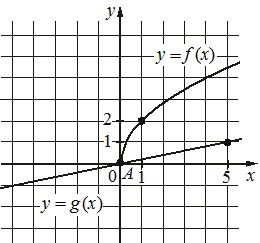
На рисунке изображены графики функций \(f(x)=a\sqrt{x}\) и \(g(x)=kx\), которые пересекаются в точках A и B. Найдите абсциссу точки B.

​

Найдите точку минимума функции \(y=(7x^2-21x-21)e^{x+12}\)

а) Решите уравнение \(2\sin^2x+\sqrt2\sin(2\pi-x)+\sqrt3\sin2x=\sqrt6\cos x\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-\pi;\dfrac{\pi}{2}\right]\)

Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.

а)

б)

В правильной треугольной призме ABCA₁B₁C₁ известно, что AB=2. Плоскость α проходит через вершины A₁ и B и середину M ребра CC₁.
а) Докажите, что сечение призмы ABCA₁B₁C₁ плоскостью α является равнобедренным треугольником.
б) Найдите высоту призмы, если площадь сечения плоскостью α равна 6.

Решите неравенство \(7\log_3(x^2-7x+12)\leqslant8+\log_3\dfrac{(x-3)^7}{x-4}\)

Строительство нового завода стоит 159 млн рублей. Затраты на производство \(x\) тыс. ед. продукции на таком заводе равны \(0{,}5x^2+2x+6\) млн рублей в год. Если продукцию завода продать по цене \(p\) тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит \(px-(0{,}5x^2+2x+6)\). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При этом в первый год \(p=10\), а далее каждый год возрастает на 1. За сколько лет окупится строительство?

Сумма оснований трапеции равна 13, а её диагонали равны 5 и 12.
а) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите высоту трапеции.

Найдите все значения \(a\), при каждом из которых уравнение \(x^4+(a-3)^2=|x-a+3|+|x+a-3|\) имеет не более одного решения.

В группе поровну юношей и девушек. Юноши отправляли электронные письма девушкам. Каждый юноша отправил или 4 письма, или 21 письмо, причём и тех и других юношей было не менее двух. Возможно, что какой-то юноша отправил какой-то девушке несколько писем.
а) Могло ли оказаться так, что каждая девушка получила ровно 7 писем?
б) Какое наименьшее количество девушек могло быть в группе, если известно, что все они получили писем поровну?
в) Пусть все девушки получили различное количество писем (возможно, какая-то девушка не получила писем вообще). Какое наибольшее количество девушек в такой группе?

Введите ответ в форме строки "да;123;1234". Где ответы на пункты разделены ";", и первый ответ с маленькой буквы.