Реальные варианты ЕГЭ
Меню курса
Основная волна ЕГЭ 2020 (вариант 1)
В пачке 250 листов бумаги формата А4. За неделю в офисе расходуется 700 листов. Какого наименьшего количества пачек бумаги хватит на 8 недель?
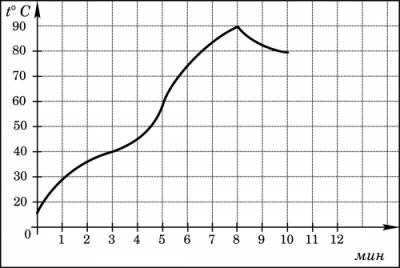
На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее с момента запуска двигателя, на оси ординат – температура двигателя в градусах Цельсия. Определите по графику, сколько минут двигатель нагревался от температуры 40°C до температуры 60°C.
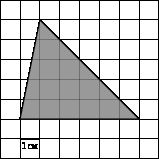
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки \(1 см× 1 см\) (см. рис.). Ответ дайте в квадратных сантиметрах.
В группе туристов 8 человек. С помощью жребия они выбирают двух человек, которые должны идти к реке за водой. Какова вероятность того, что турист А., входящий в состав группы, пойдет за водой?
Найдите корень уравнения \(3^{2-x}=81\)
Два угла вписанного в окружность четырёхугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
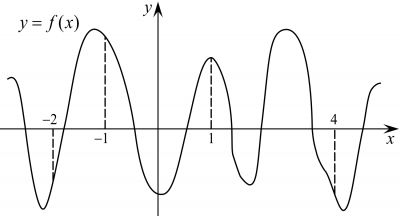
На рисунке изображен график функции \(y=f(x)\) и отмечены точки −2, −1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
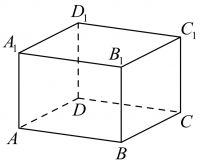
Найдите объем многогранника, вершинами которого являются точки A, B, C, B₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁, у которого AB=3, AD=3, AA₁=4.
Найдите значение выражения \(36\sqrt6 \mathrm{tg\,}\dfrac{\pi}{6}\sin\dfrac{\pi}{4}\)
Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением \(a\) км/ч². Скорость вычисляется по формуле \(v=\sqrt{2la}\), где \(l\) — пройденный автомобилем путь. Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав 0,5 километра, приобрести скорость 80 км/ч. Ответ выразите в км/ч².
Теплоход проходит по течению реки до пункта назначения 200 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 15 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 40 часов после отплытия из него. Ответ дайте в км/ч.
Найдите точку минимума функции \(y=(3-x)e^{3-x}\).
а) Решите уравнение \(\cos2x+\sqrt2\cos\left(\dfrac{\pi}2-x\right)-1=0\).
б) Укажите все корни этого уравнения, принадлежащие отрезку \(\left[\dfrac{5\pi}{2}; 4\pi\right]\)
Запишите номера всех верных ответов на пункты а) и б) по возрастанию, через запятую, без пробелов. В первое поле на пункт а), во второе - на пункт б)
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 5π/2 | 18. 8π/3 | 19. 11π/4 | 20. 17π/6 |
| 21. 3π | 22. 19π/6 | 23. 13π/4 | 24. 10π/3 |
| 25. 7π/2 | 26. 11π/3 | 27. 15π/4 | 28. 23π/6 |
| 29. 4π |
В правильной шестиугольной пирамиде SABCDEF боковое ребро SA=14, а ребро AB=8. Точка М середина ребра AB. Плоскость α проходит через точки M и D и перпендикулярна плоскости ABC. Прямая SC пересекает плоскость α в точке K.
a) Докажите, что MK = KD.
б) Найдите обьем пирамиды MCDK.
Решите неравенство \(x^2\log_{243}(4-x)\leqslant\log_3(x^2-8x+16)\)
Две окружности касаются внутренним образом в точке С. Вершины A и B равнобедренного прямоугольного треугольника ABC c прямым углом C лежат на большей и меньшей окружностях соответственно. Прямая AC вторично пересекает меньшую окружность в точке D. Прямая BC вторично пересекает большую окружность в точке E.
а) Докажите, что AE параллельно BD.
б) Найдите AC, если радиусы окружностей равны 8 и 15.
В июле 2020 года планируется взять кредит на некоторую сумму. Условия возврата таковы:
— в январе каждого года долг увеличивается на 30% по сравнению с предыдущим годом;
— с февраля по июнь нужно выплатить часть долга одним платежом.
Определите, на какую сумму будет взят кредит банке, если известно, что кредит будет выплачен тремя равными платежами (за 3 года) и общая сумма выплат будет на 78030 рублей больше суммы взятого кредита.
Найдите все значения параметра \(a\), при которых система уравнений \(\begin{cases} \log_3(a-x^2)=\log_3(a-y^2)\\x^2+y^2=4x+6y\end{cases}\) имеет ровно два различных решения.
На доске написано n единиц, между некоторыми из которых поставили знаки + и посчитали сумму. Например, если изначально было написано n=12 единиц, то могла получиться, например, такая сумма: 1+11+11+111+11+1+1=147.
Все возможные ответы на пункт в) запишите по возрастанию, через запятую, без пробелов.