Ежедневные тесты
Меню курса
Февраль
Беседа ВК для обсуждения тестов: Вступить
Сложность теста - это диапазон сложности задач, которые в этот тест попали. Сложность задачи на сайте - это процент неверных ответов на неё.
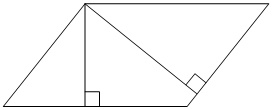
Стороны параллелограмма равны 24 и 27. Высота, опущенная на меньшую из этих сторон, равна 18. Найдите высоту, опущенную на бо́льшую сторону параллелограмма.
Даны векторы \(\vec{a}(-3;5)\) и \(\vec{b}(1;13)\). Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)
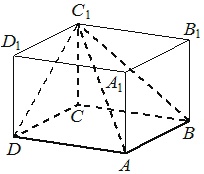
В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известно, что BC=9, CD=3, CC₁=7. Найдите объем многогранника, вершинами которого являются точки A, B, C, D, C₁.
В чемпионате по гимнастике участвуют 45 спортсменок: 6 из России, 21 из США, остальные - из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
Стрелок стреляет по одному разу в каждую из четырёх мишеней. Вероятность попадания в мишень при каждом отдельном выстреле равна 0,7. Найдите вероятность того, что стрелок попадёт в первую мишень и не попадёт в три последние.
Найдите корень уравнения \(\log_7(1-x)=\log_75\)
Найдите значение выражения \(\log_256-\log_27\)
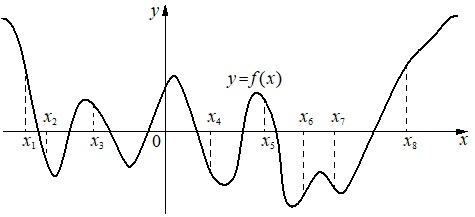
На рисунке изображен график функции y = f(x) и восемь точек на оси абсцисс: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈. В скольких из этих точек производная функции f(x) положительна?
Водолазный колокол, содержащий в начальный момент времени \(\nu=3\) моль воздуха объёмом \(V_1=16\) л, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного объёма \(V_2\) (в л). Работа (в Дж), совершаемая водой при сжатии воздуха, вычисляется по формуле \(A=a\nu T\log_{2}{\frac{V_1}{V_2}}\), где \(a=9{,}9\) Дж/моль⋅К - постоянная, а \(T=300\) К — температура воздуха. Найдите, какой объём \(V_2\) станет занимать воздух в колоколе, если при сжатии воздуха была совершена работа в 26730 Дж. Ответ дайте в литрах.
Юля и Уля, работая вместе, пропалывают грядку за 24 минуты, а одна Уля — за 120 минут. За сколько минут пропалывает эту грядку одна Юля?
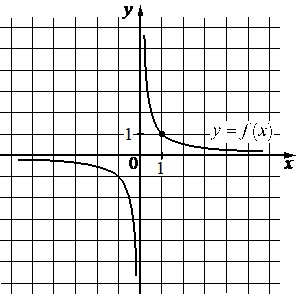
На рисунке изображен график функции вида \(f(x)=\dfrac{k}{x}\). Найдите значение \(f(10)\)
Найдите точку максимума функции \(y=3{,}5x^2-29x+30\ln x+67\)
а) Решите уравнение \(2\sin^2\left(\dfrac{\pi}2-x\right)+\sin2x=0\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[ 3\pi;\dfrac{9\pi}2\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 3π | 18. 19π/6 | 19. 13π/4 | 20. 10π/3 |
| 21. 7π/2 | 22. 11π/3 | 23. 15π/4 | 24. 23π/6 |
| 25. 4π | 26. 25π/6 | 27. 17π/4 | 28. 13π/3 |
| 29. 9π/2 |
В пирамиде SABCD с высотой SA основанием является квадрат ABCD, точка K — середина ребра SB. Прямая DK пересекается с плоскостью SAC в точке N.
a) Докажите, что прямая a, проходящая через точку N параллельно прямой SC, делит диагональ основания AC в отношении 1:2.
б) Найдите угол между прямыми DK и SC, если AB=2√3, SA=6.
Решите неравенство \(\dfrac{105}{\left(2^{4-x^2}-1\right)^2}-\dfrac{22}{2^{4-x^2}-1}+1\geqslant0\)
15 января планируется взять кредит в банке на 49 месяцев. Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Какую сумму в рублях планируется взять в кредит, если общая сумма выплат после полного его погашения составит 2 млн рублей?
(Считайте, что округления при вычислении платежей не производятся.)
Окружность с центром в точке O пересекает каждую из сторон трапеции ABCD в двух точках. Четыре получившиеся хорды окружности равны.
а) Докажите, что биссектрисы всех углов трапеции пересекаются в одной точке.
б) Найдите высоту трапеции, если окружность пересекает боковую сторону AB в точках K и L так, что AK=13, KL=6, LB=1.
Найдите все значения \(a\), при каждом из которых система неравенств \(\begin{cases}(a-x)^2+(y+a)^2\leqslant a+3\\x-y\leqslant|3-2a|\end{cases}\) имеет единственное решение.
Сторона квадрата на 3 см длиннее ширины прямоугольника, площади этих фигур равны, а все стороны – целые числа.
В пункте в перечислите возможные длины стороны квадрата по возрастанию через точку с запятой без пробелов.