7 вариант Ященко ЕГЭ 2020

Флакон шампуня стоит 160 рублей. Какое наибольшее количество флаконов можно купить на 700 рублей во время распродажи, когда скидка составляет 35%?

На диаграмме показан курс австралийского доллара, установленный Центробанком РФ на все рабочие дни марта 2019 года. По горизонтали указаны числа месяца, по вертикали — цена австралийского доллара в рублях.

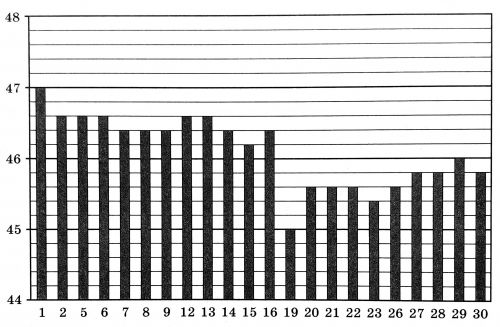
Определите, на сколько рублей стала ниже цена австралийского доллара на конец марта по сравнению с началом марта 2019 года.

На клетчатой бумаге с размером клетки \(1\times1\) изображён квадрат. Найдите его площадь.

Два автомобилиста, независимо друг от друга, выезжают из пункта А в пункт В. Навигатор предлагает каждому из них 5 равноценных маршрутов, и автомобилисты выбирают маршрут случайным образом. Найдите вероятность того, что автомобилисты выберут один и тот же маршрут.

Найдите корень уравнения \(3\dfrac{5}{9}x=5\dfrac{1}{3}\).

Основания трапеции равны 15 и 26. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Материальная точка движется прямолинейно по закону \(x(t)=t^2-9t-22\), где \(x\) – расстояние от точки отсчёта в метрах, \(t\) – время в секундах, прошедшее с начала движения. В какой момент времени (в секундах) её скорость была равна 3 м/с?

От треугольной пирамиды, объём которой равен 42, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объём отсечённой треугольной пирамиды.

Найдите значение выражения \(\dfrac{\log_{3}{4}}{\log_{3}{2}}+\log_{2}{0{,}5}\)

Расстояние от наблюдателя, находящегося на небольшой высоте \(h\) км над землёй, до наблюдаемой им линии горизонта вычисляется по формуле \(l=\sqrt{2Rh}\), где \(R=6400\) км - радиус Земли. С какой высоты горизонт виден на расстоянии 64 км? Ответ выразите в километрах.

Смешав 31-процентный и 57-процентный растворы кислоты и добавив 10 кг чистой воды, получили 22-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 47-процентный раствор кислоты. Сколько килограммов 31-процентного раствора использовали для получения смеси?

Найдите наименьшее значение функции \(y=-9-8\sqrt{3}\pi+24\sqrt{3}x-48\sqrt{3}\sin x\) на отрезке \(\left[0;\dfrac{\pi}{2}\right]\)

а) Решите уравнение \(24\cdot4^{x-0{,}5}-11\cdot2^{x+1}+6=0\)

б) Найдите все корни этого уравнения, принадлежащие промежутку [-1; 1].

Основанием пирамиды SABCD является прямоугольник ABCD со сторонами AB=15 и BC=25. Все боковые рёбра пирамиды равны \(5\sqrt{17}\). На рёбрах AD и BC отмечены соответственно точки K и N так, что AK=CN=8. Через точки K и N проведена плоскость \(\alpha\), перпендикулярная ребру SB.
а) Докажите, что плоскость \(\alpha\) проходит через точку M – середину ребра SB.
б) Найдите расстояние между прямыми DS и KM.

Решите неравенство \(\sqrt{x+\dfrac{1}{2}}\cdot\log_{\frac{1}{2}}{(\log_{2}{|1-x|})}\geqslant0\)

Четырёхугольник ABCD вписан в окружность радиуса R=27. Известно, что AB=BC=CD=36.
а) Докажите, что прямые BC и AD параллельны.
б) Найдите AD.

По бизнес-плану четырёхлетний проект предполагает начальное вложение — 25 млн рублей. По итогам каждого года планируется прирост вложенных средств на 20% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей и в первый, и во второй годы, а также целое число m млн рублей и в третий, и в четвёртый годы. Найдите наименьшее значение n, при котором первоначальные вложения за два года как минимум удвоятся, и наименьшее значение m, такое, что при найденном ранее значении n первоначальные вложения за четыре года вырастут как минимум в четыре раза.

Запишите значения n и m через точку с запятой без пробелов.

Найдите все значения \(a\), при каждом из которых линии \(y=a|x-2|+|a|-2\) и \(y=\dfrac{a}{2}\)ограничивают многоугольник, площадь которого не более 0,5.

Издательство на выставку привезло несколько книг для продажи (каждую книгу привезли в единственном экземпляре). Цена каждой книги — натуральное число рублей. Если цена книги меньше 100 рублей, на неё приклеивают бирку «выгодно». Однако до открытия выставки цену каждой книги увеличили на 10 рублей, из-за чего количество книг с бирками «выгодно» уменьшилось.
а) Могла ли уменьшиться средняя цена книг с биркой «выгодно» после открытия выставки по сравнению со средней ценой книг с биркой «выгодно» до открытия выставки?
б) Могла ли уменьшиться средняя цена книг без бирки «выгодно» после открытия выставки по сравнению со средней ценой книг без бирки «выгодно» до открытия выставки?
в) Известно, что первоначально средняя цена всех книг составляла 110 рублей, средняя цена книг с биркой «выгодно» составляла 81 рубль, а средняя цена книг без бирки – 226 рублей. После увеличения цены средняя цена книг с биркой «выгодно» составила 90 рублей, а средняя цена книг без бирки – 210 рублей. При каком наименьшем количестве книг такое возможно?

Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.