4 вариант ЕГЭ Ященко 2022

Решите уравнение \(  \dfrac{7x}{3x^2-26}=1   \). Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Из множества натуральных чисел от 56 до 80 (включительно) наудачу выбирают одно число. Какова вероятность того, что оно делится на 4?

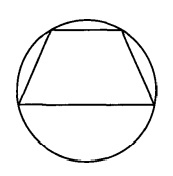
Боковая сторона равнобедренной трапеции равна её меньшему основанию, угол при основании равен 60\(^\circ\), большее основание равно 28. Найдите радиус описанной окружности этой трапеции.

Найдите значение выражения \(   5^{\sqrt{3}-4}\cdot 5^{1+3\sqrt{3}}:5^{4\sqrt{3}-1}\)

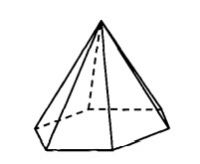
Сторона основания правильной шестиугольной пирамиды равна 3, боковое ребро равно 6. Найдите объём пирамиды.

Материальная точка движется прямолинейно по закону \(x(t)=-\dfrac{1}{2}t^4+4t^3-t^2-t+14\), где \(x\) — расстояние от точки отсчёта в метрах, \(t\) — время в секундах, прошедшее с начала движения. Найдите её скорость (в метрах в секунду) в момент времени \(t=5\) c.

Для обогрева помещения, температура в котором поддерживается на уровне \(T_п=15 °C\), через радиатор отопления пропускают горячую воду. Расход проходящей через трубу радиатора воды \(m=0{,}5\, кг/с\). Проходя по трубе расстояние \(x\), вода охлаждается от начальной температуры \(T_в=79 °C\) до температуры \(T\), причём \(x=\alpha\dfrac{cm}{γ}\log_{2}{\frac{T_в-T_п}{T-T_п}}\), где \(c=4200\,\dfrac{Вт\cdot с}{кг\cdot °C}\) - теплоёмкость воды, \(γ=63\,\dfrac{Вт}{м\cdot °C}\) - коэффициент теплообмена, а \(\alpha=1{,}3\) - постоянная. Найдите, до какой температуры (в градусах Цельсия) охладится вода, если длина трубы радиатора равна 130 м.

Имеется два сплава. Первый сплав содержит 5% никеля, второй — 14% никеля. Масса второго сплава больше массы первого на 8 кг. Из этих двух сплавов получили третий сплав, содержащий 11% никеля. Найдите массу третьего сплава. Ответ дайте в килограммах.

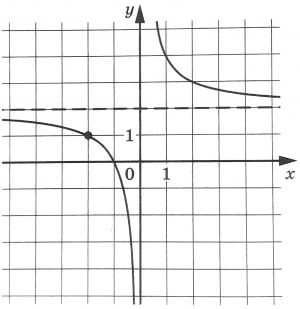
На рисунке изображен график функции \(f(x)=\dfrac{k}{x}+a\). Найдите, при каком значении \(x\) значение функции равно 7.

В торговом центре два одинаковых автомата продают чай. Вероятность того, что к концу дня в автомате закончится чай, равна 0,2. Вероятность того, что чай закончится в обоих автоматах, равна 0,18. Найдите вероятность того, что к концу дня чай останется в обоих автоматах.

Найдите наибольшее значение функции \(   y=49x-46\sin{x}+37   \) на отрезке \(\left[-\dfrac{\pi}{2};0\right]\)

а) Решите уравнение \(   25^{x-0{,}5}-13\cdot10^{x-1}+4^{x+0{,}5}=0   \).
б) Укажите корни этого уравнения, принадлежащие отрезку \(\left[-\dfrac{\pi}{2};\pi\right]\)

В правильной треугольной призме ABCA₁B₁C₁ на рёбрах AC и BC отмечены соответственно точки M и N так, что AM:MC = CN:BN = 2:1, точка K — середина ребра A₁C₁.
а) Докажите, что плоскость MNK проходит через вершину B₁.
б) Найдите расстояние от точки C до плоскости KMN, если AB = 6, AA₁ = 2,4

Решите неравенство \(8^{\lg({-1-x})}\leqslant\left( x^2-1 \right)^{\lg2}\)

По вкладу "А" банк в конце каждого года увеличивает на 10% сумму, имеющуюся на вкладе в начале года, а по вкладу "Б" — увеличивает эту сумму на 14% в течение каждого из первых двух лет. Найдите наименьшее натуральное число процентов, начисленное за третий год по вкладу "Б", при котором за все три года этот вклад будет более выгоден, чем вклад "А".

В параллелограме ABCD тангенс угла A равен 1,5. На продолжениях сторон AB и BC параллелограма за точку B выбраны точки N и M соответсвенно, причём BC=CN и AB=AM.
а) Докажите, что DN=DM.
б) Найдите MN, если AC=√13.

Найдите все положительные значения \(a\), при каждом из которых корни уравнения \(5a^{2x}-2\cdot4^x+9\cdot\left( 2a \right)^x=0\) принадлежит отрезку \(\left[-3;1\right]\).

Известно, что \(a\), \(b\), \(c\), \(d\), \(e\) и \(f\) — это различные, расставленные в некотором, возможно ином, порядке числа 2, 3, 4, 6, 7 и 16.
а) Может ли выполняться равенство \(  \dfrac{a}{b}+\dfrac{c}{d}+\dfrac{e}{f}=11 \)?
б) Может ли выполняться равенство \(  \dfrac{a}{b}+\dfrac{c}{d}+\dfrac{e}{f}=\dfrac{1345}{336} \)?
в) Какое наибольшее значение может принимать сумма \(  \dfrac{a}{b}+\dfrac{c}{d}+\dfrac{e}{f} \)?

Введите ответ в форме строки "да;да;12:34". Где ответы на пункты разделены ";", первые два ответа с маленькой буквы, в третьем несократимая дробь через двоеточие ":"