Сборники ЕГЭ профиль
Меню курса
13 вариант ЕГЭ Ященко 2021
Железнодорожный билет для взрослого стоит 480 рублей. Стоимость билета для школьника составляет 50% от стоимости билета для взрослого. Группа состоит из 14 школьников и 2 взрослых. Сколько рублей стоят билеты на всю группу?
На диаграмме показана цена серебра на момент закрытия Нью-Йоркской товарной биржи во все торговые дни мая 2019 года. По горизонтали указаны числа месяца, по вертикали — цена тройской унции серебра в долларах США.
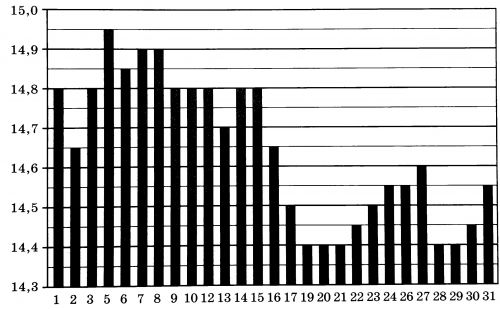
Определите по диаграмме, на сколько долларов цена тройской унции серебра 6 мая была выше, чем 26 мая.
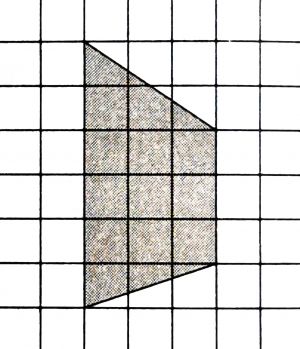
На клетчатой бумаге с размером клетки 1x1 изображена трапеция. Найдите её площадь.
Правильную игральную кость бросают дважды. Известно, что сумма выпавших очков больше 8. Найдите вероятность события «при втором броске выпало 6 очков».
Найдите корень уравнения \(\sqrt{11-5x}=1-x\). Если уравнение имеет более одного корня, в ответе запишите наибольший из корней.
Площадь параллелограмма ABCD равна 145. Найдите площадь параллелограмма A'B'C'D', вершинами которого являются середины сторон данного параллелограмма.
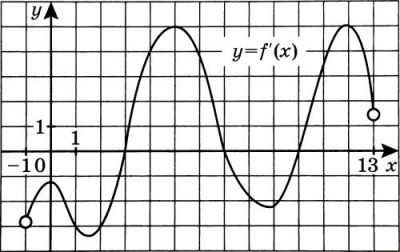
На рисунке изображён график \(y= f'(x)\) — производной функции \(f(x)\), определённой на интервале (-1; 13). Найдите количество точек, в которых касательная к графику функции \(f(x)\) параллельна прямой \(y = x + 18\) или совпадает с ней.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 188. Найдите объём конуса.
Найдите \(\log_{a}{(ab^8)}\), если \(\log_{a}{b}=8\)
Перед отправкой тепловоз издал гудок с частотой \(f_0=292\, Гц\). Чуть позже гудок издал подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка \(f\) больше первого: она зависит от скорости тепловоза по закону \(f(v)=\dfrac{f_0}{1-\dfrac{v}{c}} (Гц)\), где \(c\) - скорость звука (в м/с).Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее, чем на \(8\, Гц\). Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, a \(c=300\, м/с\). Ответ выразите в м/с.
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 16 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 10 км/ч больше скорости другого?
Найдите наибольшее значение функции \(y=(x^2+22x-22)e^{2-x}\) на отрезке [0;5].
а) Решите уравнение \(\log_{\frac{1}{2}}{(3\cos2x-2\cos^2x+5)}=-2\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[5\pi; \dfrac{13\pi}{2}\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 5π | 18. 31π/6 | 19. 21π/4 | 20. 16π/3 |
| 21. 11π/2 | 22. 17π/3 | 23. 23π/4 | 24. 35π/6 |
| 25. 6π | 26. 37π/6 | 27. 25π/4 | 28. 19π/3 |
| 29. 13π/2 |
В правильной треугольной усечённой пирамиде \(ABCA_1B_1C_1\) площадь нижнего основания \(ABC\) в четыре раза больше площади меньшего основания \(А_1B_1С_1.\) Через ребро \(AC\) проведена плоскость \(\alpha\), которая пересекает ребро \(BB_1\) в точке \(K\) и делит пирамиду на два многогранника равного объёма.
а) Докажите, что точка \(K\) делит ребро \(BB_1\) в отношении \(7:1\), считая от точки \(B\).
б) Найдите площадь сечения усечённой пирамиды плоскостью \(\alpha\), если высота пирамиды равна \(2\sqrt{2}\), а ребро меньшего основания равно \(2\sqrt{6}\).
Решите неравенство \(25^{2x^2-0{,}5}-0{,}6\cdot4^{2x^2+0{,}5}\leqslant10^{2x^2}\)
Окружность проходит через вершины \(A\), \(B\) и \(D\) параллелограмма \(ABCD\), пересекает сторону \(BC\) в точках \(B\) и \(M\), а также пересекает продолжение стороны \(CD\) за точку \(D\) в точке \(N\).
а) Докажите, что \(AM=AN\).
б) Найдите отношение \(CD:DN\), если \(AB:BC = 1:3\), а \(\cos\angle BAD=0{,}4\).
Ответ запишите в виде несократимого отношения без пробелов, например "4:13".
В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
- каждый январь долг возрастает на 15% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга, равную 1,587 млн рублей.
Сколько миллионов рублей было взято в банке, если известно, что он был полностью погашен двумя равными платежами (то есть за два года)?
Найдите все значения параметра a, при которых система уравнений
\(\begin{cases}\dfrac{(\sqrt{12-x^2}-y)\left((x+4)^2+(y+4)^2-8(x+4)+x^2-y^2-24\right)}{2-x^2}=0\\y=1-2a\end{cases}\)
имеет ровно два решения.
В школах № 1 и № 2 учащиеся писали тест. Из каждой школы тест писали по крайней мере 2 учащихся, а суммарно тест писал 51 учащийся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешёл из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах,
а) Мог ли средний балл в школе № 1 вырасти в 2 раза?
б) Средний балл в школе № 1 вырос на 10 %, средний балл в школе № 2 также вырос на 10 %. Мог ли первоначальный средний балл в школе № 2 равняться 1?
в) Средний балл в школе № 1 вырос на 10 %, средний балл в школе № 2 также вырос на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.