Сборники ЕГЭ профиль
Меню курса
1 вариант Лысенко 2022
Найдите корень уравнения \(\left(\dfrac{1}{6} \right)^{x+5}=6^x\)
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 5 очков. Ответ округлите до сотых.
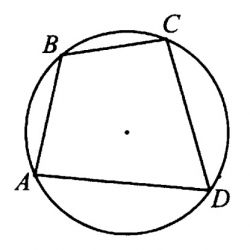
Стороны AB, BC, CD и AD четырёхугольника ABCD стягивают дуги описанной окружности, градусные величины которых равны соответственно 75°, 63°, 93°, 129°. Найдите угол BCD. Ответ дайте в градусах.
Найдите значение выражения \(11\sqrt{3} \mathrm{tg\dfrac{7\pi}{6}}\cdot\cos{\dfrac{4\pi}{3}} \)
Площадь поверхности куба равна 72. Найдите его диагональ.
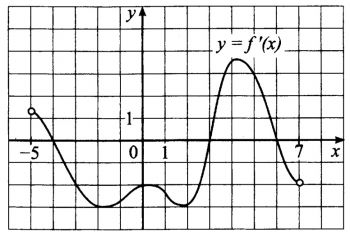
На рисунке изображен график y=f'(x) — производной f(x), определённой на интервале (-5;7). В какой точке отрезка [-3;2] функция f(x) принимает наименьшее значение?
При температуре \(0^\circ\) \(C\) рельс имеет длину \(l_{0}=10\)м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону \(l(t_{0}) = l_{0}(1+\alpha\cdot t^{\circ})\), где \(\alpha=1{,}2 \cdot10^{-5}(^{\circ}C)^{-1}\) — коэффициент теплового расширения, \(t^\circ\) — температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ дайте в градусах Цельсия.
Из двух городов A и B, расстояние между которыми равно 360 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 135 км от города B. За сколько часов автомобиль, выехавший из города A, доедет до города B?
График функции \(y=\dfrac{k}{x}+b\) проходит через точки \(\left (6;8\right)\) и \(\left (-2;12\right)\). Найдите \(b\).
Телефон передаёт SMS-сообщение. В случае неудачи он делает следующую попытку. Вероятность того, что SMS-сообщение удастся передать без ошибок, в ходе каждой отдельной попытки равна 0,5. Найдите вероятность того, что для передачи собщения потребуется не больше трёх попыток.
Найдите точку максимума функции \(y=\ln({x+6})-4x+11\).
а) Решите уравнение \(2\cos\left({\dfrac{3\pi}{2}-x}\right)\cdot\sin\left({\dfrac{\pi}{2}-x}\right)=\sqrt{3}\sin({2\pi+x})\)
б) Найдите корни данного уравнения, принадлежащие отрезку \(\left[-\dfrac{11\pi}{2};-3\pi\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -11π/2 | 18. -16π/3 | 19. -21π/4 | 20. -31π/6 |
| 21. -5π | 22. -29π/6 | 23. -19π/4 | 24. -14π/3 |
| 25. -9π/2 | 26. -13π/3 | 27. -17π/4 | 28. -25π/6 |
| 29. -4π | 30. -23π/6 | 31. -15π/4 | 32. -11π/3 |
| 33. -7π/2 | 34. -10π/3 | 35. -13π/4 | 36. -19π/6 |
| 37. -3π |
В правильной четырёхугольной пирамиде SABCD сторона основания AB = 10, а боковое ребро SA = 15. На рёбрах AB и SB отмечены точки M и K соответственно, причём AM = 40/7, SK = 6.
а) Докажите, что плоскость CKM перпендикулярна плоскости ABC.
б) Найдите объём пирамиды BCKM.
Решите неравенство \(7\log_{12}({x^2-2x-8})\leqslant 8+\log_{12}{\dfrac{(x+2)^7}{x-4}}\)
В сентябре планируется взять кредит в банке на сумму 3 млн рублей на некоторый срок. Условия его возврата таковы:
- каждый январь долг возрастает на 15% по сравнению с концом предыдущего года;
- с февраля по август каждого года нужно выплачивать часть долга;
- в сентябре каждого года долг должен быть на одну и ту же величину меньше долга на сентябрь предыдущего года.
На какой минимальный срок (целое число лет) следует брать кредит, чтобы наибольший годовой платёж по кредиту не превысил 0,96 млн рублей?
В прямоугольном треугольнике ABC точка D лежит на катете AC, а точка F — на продолжении катета BC за точку C, причём CD = BC и CF = AC. Отрезки CM и CN — высоты треугольников ABC и FCD соответственно.
а) Докажите, что CM и CN перпендикулярны.
б) Прямые AF и BD пересекаются в точке K. Найдите DK, если BC = 3, AC = 9.
Найдите все значения параметра \(a\), при каждом из которых уравнение \(\dfrac{x^2-8x-2a}{11x^2-8ax-3a^2}=0\) имеет ровно два различных решения.
Костя написал на доске несколько различных натуральных чисел, каждое из которых делится нацело на 7 и оканчивается на 8.